考研数学二（线性代数）模拟试卷96

考研数学二（线性代数）模拟试卷96

选择题

1.设A=(B)

A. x=2，y=4，z=8

B. x=﹣1，y=4，z∈R

C. x=﹣2，y=2，z∈R

D. x=﹣1，y=4，z=3

解析：利用矩阵与特征值的关系，即由丨A丨=λ₁λ₂…λ_n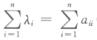，(矩阵的迹)确定矩阵中待定参数，是常用的一种方法．但当未知参数较多时，则应该采用更为一般的特征多项式丨λE﹣A丨=(λ﹣λ₁)(λ﹣λ₂)…(λ﹣λ_n)确定．本题由于未知量较多，采用的是后一种方法，即由

丨λE﹣A丨=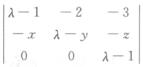

2.已知α₁=[﹣1，1，a，4]^T，α₂=[﹣2，1，5，a]^T，α₃=[a，2，10，1]^T是4阶方阵A的3个不同特征值对应的特征向量，则a的取值范围为( )．(A)

A. a≠5

B. a≠﹣4

C. a≠﹣3

D. a≠﹣3且a≠﹣4

解析：α₁，α₂，α₃是3个不同特征值对应的特征向量，必线性无关，由

3.设矩阵A满足A³﹣A²=A﹣E，则( )．(D)

A. A+E与A﹣E都不可逆

B. A+E与A﹣E至少有一个可逆

C. A+E与A﹣E有且仅有一个可逆

D. A+E与A﹣E至多有一个可逆

解析：由A³﹣A²=A﹣E，得(A+E)(A﹣E)²=O，故矩阵A的特征值只可能为1或﹣1．若A的特征值全为1，则A+E的特征值全为2，A﹣E的特征值全为0，从而A+E可逆，而A﹣E不可逆；若A的特征值全为﹣1，则A+E的特征值全为0，A﹣E的特征值全为﹣2，从而A﹣E可逆，而A+E不可逆；若1与﹣1都是A的特征值，则A+E与A﹣E都有一个特征值为0，从而A+E与A﹣E都不可逆．由此可见，A+E与A﹣E至多有一个可逆．应选(D)．

4.已知A是3阶矩阵，r(A)=1，则λ=0( )．(B)

A. 必是A的二重特征值

B. 至少是A的二重特征值

C. 至多是A的二重特征值

D. 是一重、二重、三重特征值都可能

解析：A是3阶矩阵，r(A)=1，故r(0E﹣A)=1，那么(0E﹣A)x=0有两个线性无关的解向量，故λ=0至少是二重特征值，也可能是三重特征值，例如：A=

5.设A是3阶方阵，满足丨3A+2E丨=0，丨A﹣E丨=0，丨3E﹣2A丨=0，则丨A丨=( )．(C)

A. 2

B. 1

C. ﹣1

D. ﹣2

解析：矩阵的特征值的计算一般有三种方法：第一种是由特征方程解出；第二种是由定义式推导得到；第三种是由矩阵方程转化为特征方程解方程得到．由题设均可化为A的特征方程形式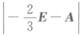=0，丨E﹣A丨=0，=0，从而可以得到A的全部特征值λ₁=﹣2／3，λ₂=1，λ₃=3／2，进一步可得到丨A丨=λ₁λ₂λ₃=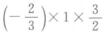

6.已知2阶实对称矩阵A的秩r(A)=1，λ₁=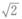是其一个特征值，ξ₁=[1，﹣1]^T为属于λ₁=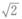的特征向量，设k为任意常数，则非齐次线性方程组Ax=ξ₁的通解是( )．

(B)

A.

B.

C.

D.

解析：A为实对称矩阵，必可相似对角化．又r(A)=1，故由λ₁=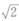≠0，有λ₂=0．因不同特征值对应的特征向量正交，而[1，﹣1]本文档预览：3000字符，共12100字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载