
考研数学二(线性代数)模拟试卷94
选择题
1.设A是m×n矩阵,B是n×m矩阵,若满足AB=E,其中E是m阶单位矩阵,则( ).(C)
A. A的列向量组线性无关,B的行向量组线性无关
B. A的列向量组线性无关,B的列向量组线性无关
C. A的行向量组线性无关,B的列向量组线性无关
D. A的行向量组线性无关,B的行向量组线性无关
解析:因为AB=E,且A是m×n矩阵,B是n×m矩阵,故r(AB)=r(E)=m.于是,m≥r(A)≥r(AB)=m,m≥r(B)≥r(AB)=m,故r(A)=r(B)=m这表明A的行向量组线性无关,B的列向量组线性无关.故应选(C).
2.设向量组(Ⅰ)α1,α2,…,αs线性无关,(Ⅱ)β1,β2,…,βt线性无关,且αi(i=1,2,…,s)不能由(Ⅱ)β1,β2,…,βt线性表出,βj(j=1,2,…,t)也不能由(Ⅰ)α1,α2,…,αs,线性表出,则向量组α1,α2,…,αs,β1,β2,…,βt( ).(C)
A. 必线性相关
B. 必线性无关
C. 可能线性相关,也可能线性无关
D. 以上都不正确
解析:只需对两种情况举出例子即可.
①取α1= ,α2=
,α2= 线性无关,β1=
线性无关,β1= ,β2=
,β2= 线性无关,显然不能相互线性表出,但4个3维列向量必定线性相关;
线性无关,显然不能相互线性表出,但4个3维列向量必定线性相关;
②取α1= ,α2=
,α2=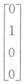 线性无关,β1=
线性无关,β1= ,β2=
,β2=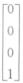
3.已知α1,α2,α3,α4为3维非零列向量,则下列结论:
①如果α4不能由α1,α2,α3线性表出,则α1,α2,α3线性相关;
②如果α1,α2,α3线性相关,α2,α3,α4线性相关,则α1,α2,α4也线性相关;
③如果r(α1,α1+α2,α2+α3)=r(α4,α1+α4,α2+α4,α3+α4),则α4可以由α1,α2,α3线性表出.
其中正确的个数为( ).(C)
A. 0
B. 1
C. 2
D. 3
解析:如果α1,α2,α3线性无关,由于α1,α2,α3,α4为4个3维列向量,故α1,α2,α3,α4线性相关,则α4必能由α1,α2,α3线性表出,可知①是正确的.
令α1= ,α2=
,α2= ,α3=
,α3= ,α4=
,α4=