考研数学二（线性代数）模拟试卷92

考研数学二（线性代数）模拟试卷92

选择题

1.设α₁，α₂，α₃均为线性方程组Ax=b的解，则下列向量

α₁﹣α₂，α₁﹣2α₂+α₃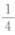，(A)

A. 4

B. 3

C. 2

D. 1

解析：由Aα₁=Aα₂=Aα₃=b，可知

A(α₁﹣α₂)=Aα₁﹣Aα₂=b﹣b=0，

A(α₁﹣2α₂+α₃)=Aα₁﹣2Aα₂+Aα₃=b﹣2b+b=0，

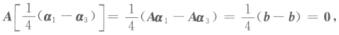
2.设n(n≥2)为正整数，A是(n﹣1)×n矩阵，划去A的第j列后构成的n﹣1阶行列式记为a_j，令b_j=(﹣1)^j-1a_j(j=1，2，…，n)．则对于n元齐次线性方程组Ax=0，下列结论一定正确的是( )．(B)

A. 向量[a₁，a₂，…，a_n]^T是Ax=0的一个解

B. 向量[b₁，b₂，…，b_n]^T是Ax=0的一个解

C. 向量[a₁，a₂，…，a_n]^T是Ax=0的一个基础解系

D. 向量[b₁，b₂，…，b_n]^T是Ax=0的一个基础解系

解析：设A=(p_ij)。则齐次线性方程组Ax=0．即

对于i=1，2，…，n﹣1，考虑n阶行列式

D_i=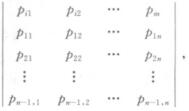

3.设A是m×n实矩阵，则对任意m维列向量b，线性方程组A^TAx=A^Tb( )．(B)

A. 无解

B. 有解

C. 必有唯一解

D. 必有无穷多解

解析：对任意m维列向量b，由于[A^TA丨A^Tb]=A^T[A丨b]，故

r([A^TA丨A^Tb])≤r(A^T)=r(A)，

又 r(A)=r(A^TA)≤r([A^TA丨A^Tb])，

故r(A^TA)=r([A^TA丨A^Tb)，因此A^TAx=A^Tb有解．由于不知A^TA是否列满秩，故(C)，(D)不正确，选(B)．

4.设A为n阶实矩阵，则对线性方程组(Ⅰ)Ax=0和(Ⅱ)A^TAx=0，必有( )．(A)

A. (Ⅱ)的解是(Ⅰ)的解，(Ⅰ)的解也是(Ⅱ)的解

B. (Ⅱ)的解是(Ⅰ)的解，但(Ⅰ)的解不是(Ⅱ)的解

C. (Ⅰ)的解不是(Ⅱ)的解，(Ⅱ)的解也不是(Ⅰ)的解

D. (Ⅰ)的解是(Ⅱ)的解，但(Ⅱ)的解不是(Ⅰ)的解

解析：方程组At=0和A^TAx=0是同解方程组(注意到x^TA^TAx=(Ax)^TAx≥0)．

5.设A是4阶矩阵，向量α，β是齐次线性方程组(A﹣E)x=0的一个基础解系，向量γ是齐次线性方程组(A+E)x=0的一个基础解系．则齐次线性方程组(A²﹣E)X-0的通解为( )．(D)

A. C₁α+C₂β，其中C₁，C₂为任意常数

B. C₁α+C₂γ，其中C₁，C₂为任意常数

C. C₁β+C₂γ，其中C₁，C₂为任意常数

D. C₁α+C₂β+C₃γ，其中C₁，C₂，C₃为任意常数

解析：首先，证明α，β，γ线性无关．

方法一 根据题设条件，α，β是A的属于特征值λ=1的两个线性无关的特征向量，γ是A的属于特征值λ=﹣1的一个特征向量，由于属于不同特征值的线性无关的特征向量组，合起来仍然线性无关，因此α，β，γ线性无关．

方法二 令k₁α+k₂β+k₃γ=0，两边左乘A﹣E，并利用条件(A﹣E)α=0，(A﹣E)β=0及Aγ=﹣γ，得k₃(A﹣E)γ=0，从而有k₃γ=0，

本文档预览：3000字符，共13091字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载