考研数学二（线性代数）模拟试卷95

考研数学二（线性代数）模拟试卷95

选择题

1.设A为n阶矩阵，下列结论正确的是( )．(A)

A. A可逆的充分必要条件是其所有特征值非零

B. A的秩等于非零特征值的个数

C. A和A^T有相同的特征值和相同的特征向量

D. 若A与同阶矩阵B有相同特征值，则两矩阵必相似

解析：由丨A丨=A=λ₁λ₂…λ_n知，A可逆的充分必要条件是其所有特征值非零，但一般地，A的秩与其非零特征值的个数未必相等，如矩阵A=

2.设矩阵A=(C)

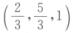A. B. 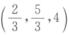C. (2，1，1)

D. (2，2，4)

解析：丨A丨=3a﹣2，A^*α=λα，又由AA^*=丨A丨E，有A^*α=丨A丨α=λAα，即可得

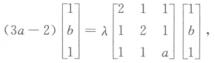
即

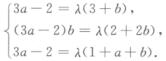
又3a﹣2≠0，λ≠0，故可解得

3.设λ₁，λ₂是n阶矩阵A的特征值，α₁，α₂分别是A的对应于λ₁，λ₂的特征向量，则( )．(D)

A. 当λ₁=λ₂时，α₁，α₂对应分量必成比例

B. 当λ₁=λ₂时，α₁，α₂对应分量必不成比例

C. 当λ₁=≠λ₂时，α₁，α₂对应分量必成比例

D. 当λ₁≠λ₂时，α₁，α₂对应分量必不成比例

解析：当λ₁=λ₂时，α₁与α₂可能线性相关也可能线性无关，所以α₁，α₂对应分量可能成比例，也可能不成比例，故排除(A)，(B)．当λ₁≠λ₂时，α₁，α₂一定线性无关，对应分量一定不成比例，故选(D)．

4.设A为n阶矩阵，则下列命题正确的是( )．(D)

A. 若α为A^T的特征向量，那么α为A的特征向量

B. 若α为A^*的特征向量，那么α为A的特征向量

C. 若α为A²的特征向量，那么α为A的特征向量

D. 若α为2A的特征向量，那么α为A的特征向量

解析：矩阵A^T与A的特征值相同，但特征向量不一定相同，故(A)不正确．

假设α为A的特征向量，λ为其特征值，当λ≠0时，α也为A^*的特征向量．这是由于

Aα=λαA^*Aα=λA^*αA^*α=λ^-1丨A丨α．

但反之，α为A^*的特征向量，那么α不一定为A的特征向量．例如：当r(A)＜n﹣1时，A^*=O，此时，任意n维非零列向量都是A^*的特征向量，故A^*的特征向量不一定是A的特征向量．可知(B)不正确．

假设α为A的特征向量，λ为其特征值，则α为A²的特征向量．这是由于

A²α=A(Aα)=λAα=λ²α．

但反之，若α为A²的特征向量，α不一定为A的特征向量．例如：假设Aβ₁=β₁，Aβ₂=﹣β₂，其中β₁，β₂≠0．此时有A²(β₁+β₂)=A²β₁+A²β₂=β₁+β₂，可知β₁+β₂为A²的特征向量．但β₁，β₂是矩阵A两个不同特征值的特征向量，它们的和β₁+β₂本文档预览：3000字符，共16512字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载