考研数学二（线性代数）模拟试卷93

考研数学二（线性代数）模拟试卷93

选择题

1.设ξ₁=[1，﹣2，3，2]^T，ξ₂=[2，0，5，﹣2]^T是齐次线性方程组Ax=0的基础解系，则下列向量中是齐次线性方程组Ax=0的解向量的是( )．(C)

A. α₁=[1，﹣3，3，3]^T

B. α₂=[0，0，5，﹣2]^T

C. α₃=[﹣1，﹣6，﹣1，10]^T

D. α₄=[1，6，1，0]^T

解析：已知Ax=0的基础解系为ξ₁，ξ₂，则α_i(i=1，2，3，4)是Ax=0的解向量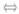α_i可由ξ₁，ξ₂线性表出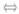非齐次线性方程组y₁ξ₁+y₂ξ₂=α_i有解．逐个判别α_i较麻烦，合在一起作初等行变换判别较方便．

2.设α₁，α₂，α₃，α₄，α₅均是4维列向量，记A=[α₁，α₂，α₃，α₄]，B=[α₁，α₂，α₃，α₄，α₅]．已知方程组AX=α₅有通解k[1，﹣1，2，0]^T+[2，1，0，1]^T，其中k是任意常数，则下列向量不是方程组Bx=0的解的是( )．(A)

A. [1，﹣2，﹣2，0，﹣1]^T

B. [0，3，﹣4，1，﹣1]^T

C. [2，1，0，1，﹣1]^T

D. [3，0，2，1，﹣1]^T

解析：由Ax=α₅的通解k[1，﹣1，2，0]^T+[2，1，0，1]^T知，α₅可由α₁，α₂，α₃，α₄线性表出为

α₅=(k+2)α₁+(﹣k+1)α₂+2kα₃+α₄，

即 (k+2)α₁+(﹣k+1)α₂+2kα₃+α₄﹣α₅=0，

故 [α₁，α₂，α₃，α₄，α₅]=[α₁，α₂，α₃，α₄，α₅]

3.齐次线性方程组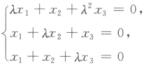(C)

A. λ=﹣2且丨B丨=0

B. λ=﹣2且丨B丨≠0

C. λ=1且丨B丨=0

D. λ=1且丨B丨≠0

解析：B≠0，AB=0，故Ax=0有非零解，所以丨A丨=0，即

丨A丨=

4.设A是m×s矩阵，B是s×n矩阵，则齐次线性方程组Bx=0和ABx=0是同解方程组的一个充分条件是( )．(B)

A. r(A)=m

B. r(A)=s

C. r(B)=s

D. r(B)=n

解析：显然Bx=0的解必是ABx=0的解．又因r(A)=s，即A的列向量组线性无关，从而若Ay=0，则必有y=0(即Ay=0只有零解)．故若ABx=0必有Bx=0，即ABx=0的解也是Bx=0的解，故选(B)．

5.设A与B均为n阶方阵，则方程组Ax=0与Bx=0有非零公共解的一个充分条件是( )．(C)

A. r(A)=r(B)

B. r(A)+r(B)≤n

C. r(A)+r(B)＜n

D. n＜r(A)+r(B)＜2n

解析：构造齐次线性方程组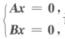设α₁，α₂，…，α_r与β₁，β₂，…，β_t分别是矩阵A与矩阵B的行向量组的极大线性无关组，则矩阵本文档预览：3000字符，共12798字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载