考研数学二（线性代数）模拟试卷87

考研数学二（线性代数）模拟试卷87

选择题

1.设A为3阶非零矩阵，且满足a_ij=A_ij(i，j=1，2，3)，其中A_ij为a_ij的代数余子式，则下列结论中：

①A是可逆矩阵； ②A是对称矩阵； ③A是不可逆矩阵； ④A是正交矩阵．

正确的个数为( )．(B)

A. 1

B. 2

C. 3

D. 4

解析：由a_ij=A_ij(i，j=1，2，3)及伴随矩阵的定义可知A^*=A^T，那么丨A^*丨=丨A^T丨，即丨A丨²=丨A丨，也即丨A丨(丨A丨﹣1)=0．

又由于A为非零矩阵，不妨设a₁₁≠0，则

丨A丨=a₁₁A₁₁+a₁₂A₁₂+a₁₃A₁₃=a₁₁²+a₁₂²+a₁₃²＞0，

故丨A丨=1．因此A可逆．

并且AA^T=AA^*=丨A丨E=E，于是A是正交矩阵．于是①，④正确，③错误．

从题目中的条件无法判断A是否为对称矩阵，故正确的只有2个，选(B)．

2.已知A，B为同阶可逆矩阵，则( )．(C)

A. (A+B)^-1=A^-1+B^-1

B. (AB)^-1=A^-1B^-1

C. (Aⁿ)^-1=(A^-1)ⁿ

D. (2A)^-1=2A^-1

解析：矩阵的逆运算是重要的矩阵运算之一，应熟练掌握其运算性质．首先，两个可逆矩阵的和A+B未必可逆，即使A+B可逆，等式(A+B)^-1=A^-1+B^-1也不一定成立．同样的，(AB)^-1=B^-1A^-1，2A^-1(2A)=4A^-1A≠E，知选项(A)，(B)，(D)均不正确，由排除法，故选(C)．

事实上，由(A^-1)ⁿAⁿ=(A^-1A)ⁿ=Eⁿ=E，知(Aⁿ)^-1=(A^-1)ⁿ．

3.A为3阶矩阵，将A的第二列加到第一列得矩阵B，再交换B的第二行与第三行得单位矩阵，记

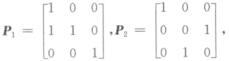(A)

A. P₁P₂

B. P₁^-1P₂

C. P₂P₁

D. P₂P₁^-1

解析：依题设，AE₂₁(1)=B，E₂₃B=E，有

A=BE₂₁^-1(1)=E₂₃^-1E₂₁^-1(1)，

进而有

A^-1=[E₂₃^-1E₂₁^-1(1)]^-1=E₂₁(1)E₂₃，

其中E₂₁(1)=P₁，E₂₃=P₂，因此选(A)．

4.设A为n阶可逆矩阵，则下列等式中，不一定成立的是( )．(B)

A. (A+A^-1)²=A²+2AA^-1+(A^-1)²

B. (A+A^T)²=A²+2AA^T+(A^T)²

C. (A+A^*)²=A²+2AA^*+(A^*)²

D. (A+E)²=A²+2AE+E²

解析：由矩阵乘法的分配律可知

(A+B)²=(A+B)A+(A+B)B=A²+BA+AB+B²，

因此，(A+B)²=A²+2AB+B²的充要条件是BA=AB，即A，B可交换．

由于A与A^-1，A与A^*以及A与E都是可交换的，因此(A)，(C)，(D)中的等式都是成立的．故选(B)．

5.设

(C)

A. A

本文档预览：3000字符，共11085字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载