考研数学二（线性代数）模拟试卷97

考研数学二（线性代数）模拟试卷97

选择题

1.设A是3阶方阵，有3阶可逆矩阵P，使得P^-1AP=，A^*是A的伴随矩阵，则P^-1A^*P=( )．

(D)

A.

B.

C.

D.

解析：方法一 设P=[ξ₁，ξ₂，ξ₃]，其中ξ₁，ξ₂，ξ₃分别是对应于A的特征值λ₁=1，λ₂=2，λ₃=3的特征向量，则ξ₁，ξ₂，ξ₃也是A^-1的分别对应于特征值μ₁=1／λ₁=1，μ₂=1／λ₂=1／2，μ₃=1／λ₃=1／3的特征向量．

因 A^*=丨A丨A^-1，丨A丨=丨PΛP^-1丨=丨Λ丨==6，

故ξ₁，ξ₂，ξ₃是A^*的分别对应于特征值l₁=丨A丨μ₁=6，l₂=丨A丨μ₂=3，l₃=丨A丨μ₃=2的特征向量．故有

P^-1A^*P=，

故应选(D)．

方法二 由P^-1AP=，两边求逆，得

(P^-1AP)^-1=P^-1A^-1(P^-1)^-1=P^-1A^-1P=，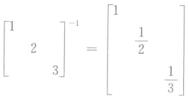

上式左右两端分别乘丨A丨(丨A丨是一个数，丨A丨==6)，得

P^-1丨A丨A^-1P=P^-1A^*P=

2.已知P^-1AP=(D)

A. [α₁，﹣α₂，α₃]

B. [α₁，α₂+α₃，α₂﹣2α₃]

C. [α₁，α₃，α₂]

D. [α₁+α₂，α₁﹣α₂，α₃]

解析：若P^-1AP=Λ=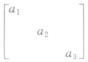，P=[ξ₁，ξ₂，ξ₃]，则有AP=PA，即

A[ξ₁，ξ₂，ξ₃]=[ξ₁，ξ₂，ξ₃]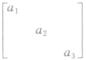

3.设A，B均为n阶矩阵，A可逆且A～B，则下列命题中：

①AB～BA； ②A²～B²； ③A^T～B^T； ④A^-1～B^-1．

正确命题的个数为( )．(D)

A. 1

B. 2

C. 3

D. 4

解析：由A～B可知，存在可逆矩阵P，使得P^-1AP=B．故

P^-1A²P=B²，P^TA^T(P^T)^-1=B^T，P^-1A^-1P=B^{本文档预览：3000字符，共15895字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}