考研数学一（概率论与数理统计）模拟试卷118
解答题
1.设随机变量x和y相互独立，X～N(0，1)，Y～U[0，1]，Z=X+Y，求Z的概率密度函数fz(z)．
X～N(0，1)，记X的分布函数为φ(x)，概率密度为[*](x)．
(X，Y)的密度函数为f(x，y)=fx(x)fY(y)=[*]
方法一 用卷积公式：
[*]
方法二
[*]
方法三 用定义法：
[*]
[*]
解析：
2.设随机变量X与Y相互独立的概率分布为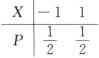
Coy(X，Y)=Cov(X，XY)=E(X2Y)-E(X)E(XY)，
其中E(X2Y)=E(X2)E(Y)=[*]
而 E(X)E(XY)=0·E(XY)=0，
所以 Cov(X，Y)=λ．
解析：
设二维随机变量(X，Y)的概率密度为
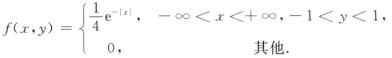
3.X与Y是否相互独立?
X，Y的边缘密度分别为
[*]
解析：
4.求Z的概率密度；
[*]
解析：
5.求Z的数学期望和方差．
[*]
解析：
6.设X～N(0，1)，试证：E(Xk)=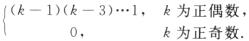
X～N(0，1)，当k为正奇数时，E(Xk)=[*]，因为xkf(x)是奇函数．
当k为正偶数时，xkf(x)是偶函数．故
[*]
当k为正偶数时，得到递推公式E(Xk)=(k-1)E(Xk-2)．
由此得E(Xk)=(k-1)(k-3)…3·E(X2)=(k-1)(k-3)…3·1．
总之E(Xk)=[*]
解析：
设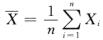
7.
[*]
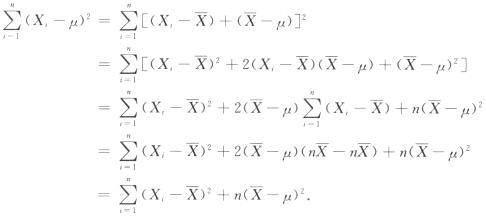
解析：
8.
[*]
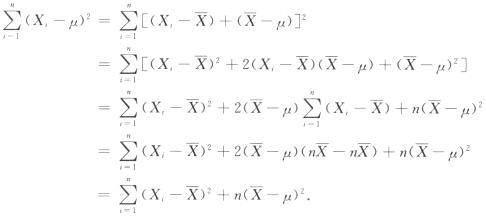
解析：
9.设总体X的概率密度为
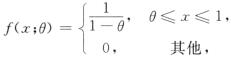
EX=[*]
令EX=[*]
似然函数 L(θ)=[*]
要使L(θ)最大，只有使1-θ尽量小，或者θ尽量接近于1．但θ≤x1，…，xn，故取
θ=min(x1，…，xn)或θ=[*]
θ的最大似然估计量为[*]
解析：
10.设随机变量X在数集{0，1，2，…，N}上等可能分布，求N的最大似然估计量．
P{X=K}=[*]，K=0，1，…,N．
[*]
L关于N是单调减函数，L最大就要求N尽量小，但对所有的Xi均有XXi≤N，i=1，…，n．要取N尽量小，只有取[*]
解析：
11.设总体X的概率分布为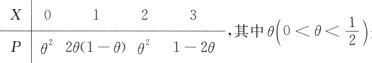
总体X的期望为
E(X)=0·θ2+1·2θ(1-θ)+2·θ2+3·(1-2θ)=3-4θ．
又样本均值为
[*]
下面求最大似然估计值．
对于给定的样本值，似然函数为L(θ)=4θ6(1-θ)2(1-2θ)4，取对数，得
ln L(θ)=ln 4+6ln θ+2ln(1-θ)+4ln(1-20)，
求导，有[*]
令[*]不合题意，舍去．
所以θ的最大似然估计值为[*]
解析：
选择题
12.设A，B为两个随机事件，且0＜P(A)＜1，0＜P(B)＜1，则P(A | B)=l的充分必要条件是(C)
A. P(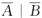
B. P(B | A)=1
C. P(
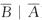D. P(
本文档预览：3000字符，共12192字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
