
考研数学一(概率论与数理统计)模拟试卷116
解答题
设二维随机变量(X,Y)的概率密度为
f(x,y)=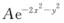
1.求常数A;
方法一 二维正态分布(X,Y)~N(μ1,μ2;σ12,σ22;ρ)的密度为
[*]
对比本题所给密度f(x,y)=[*],不难看出题给分布为二维正态分布:
[*]
方法二
[*]
解析:
2.求条件概率密度fY|X(y | x).
显然X,Y是相互独立的(因为ρ=0),所以
[*]
当0<x<1时,也就是fx(x)>0时,fY|X(y | x)=[*]
解析:
3.二维随机变量(X,Y)的概率密度为f(x,y),-∞<x<+∞,-∞<y<+∞.
已知X的密度
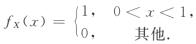
当0<x<1时,条件概率密度

当0<x<1时,fx(x)=1,所以f(x,y)=fx(x)fY|X(y | x)=fY|X(y | x).
我们得到,当0<x<1时,f(x,y)=[*]
但f(x,y)应该是定义在全平面上,且[*]
显然在0<x<1时,[*]
所以,可以理解x<0或x>1时,f(x,y)≡0.
即可将f(x,y)=[*]
改写为[*]
解析:
4.设随机变量X与Y相互独立,且X的分布为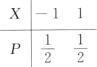
[*]
解析:
设随机变量X1,X2相互独立,X1~E(1),X2~E(λ)(λ>0)·令Y=min{X1,X2},Z=max{X1,1}.
5.求Y的概率密度fY(y);
Y的分布函数为
[*]
解析:
6.
[*]
解析:
7.求Z的数学期望E(Z).
[*]
解析:
设总体X~U(μ,σ2),X1,X2,…,Xn是来自总体X的样本,记Y=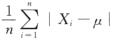
8.E(Y)=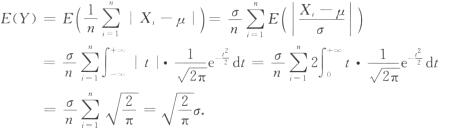
[*]
解析:
9.D(Y)=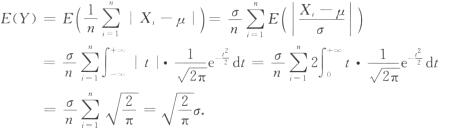
[*]
解析:
10.设X1,X2,…,Xn是来自正态总体x的简单随机样本,Y1=1/6(X1+…+X6),Y2=1/3(X7+X8+X9),S2=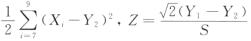
设X~N(μ,2),μ,σ2未知,则
E(Y1)=E(Y2)=μ,D(Y1)=σ2/6,D(Y2)=σ2/3.
由于Y1和Y2相互独立,故D(Y1-Y2)=[*].
而[*].Y1与S2相互独立,Y2与S2也相互独立,所以Y1-Y2与S2相互独立.
总之[*],
其中①U~N(0,1);②[*]相互独立.
解析:
选择题
11.袋中装有2n-1个白球,2n个黑球,一次取出n个球,发现都是同一种颜色,则这种颜色是黑色的概率为(D)
A. 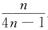 B.
B. 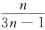 C. 1
C. 1
本文档预览:3000字符,共12517字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载