
考研数学(数学二)模拟试卷742
选择题
1.已知f(x),g(x)在x0的某去心邻域内有定义,且g(x)≠0,则下列结论中正确的是
 (C)
(C)
A.
B.
C.
D.
解析:
2.设f(x)在x=0可导,f(0)=0,f'(0)=1,F(x)= (C)
(C)
A. F(x)在x=0可导.
B. F(x)在x=0不可导,但连续.
C. x=0是F(x)的第一类间断点.
D. x=0是F(x)的第二类间断点.
解析:因为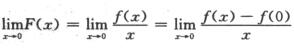
3.曲线y=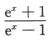 (B)
(B)
A. 4
B. 3
C. 2
D. 1
解析: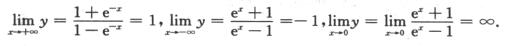
4.设f(x)在(-1,1)上二阶可导,且f'(x)>0,F(x)=∫0x(2t-x)f(t)dt,则下列结论中正确的是(C)
A. F(0)是F(x)的极大值.
B. F(0)是F(x)的极小值.
C. x=0不是F(x)的极值点,但(0,F(0))是曲线y=F(x)的拐点.
D. x=0不是F(x)的极值点,(0,F(0))也不是曲线y=F(x)的拐点.
解析:F(x)=2∫0xtf(t)dt-x∫0xf(t)dt,求导得
F'(x)=xf(x)-∫0xf(t)dt=∫0x[f(x)-f(t)]dt.
因为f'(x)>0,所以f(x)严格单增,于是当x>0时,0<t<x,f(t)<f(x),从而
F'(x)=∫0x[f(x)-f(t)]dt>0;
当x<0时,x<t<0,f(x)<f(t),从而
F'(x)=-∫x0[f(x)-f(t)]dt>0,
x=0不是F(x)的极值点.
再由F"(x)=xf'(x),f'(x)>0,可知当x>0时,F"(x)>0;当x<0时,F"(x)<0,从而
(0,F(0))是曲线y=F(x)的拐点.
故应选(C).
5.已知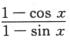 (A)
(A)
A. 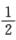 B.
B. 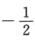 C. 2
C. 2
D. -2
解析: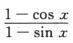 =a1x+a2x2+a3x3+o(x3),所以
=a1x+a2x2+a3x3+o(x3),所以
1-cos x=(1-sin x)[a1x+a2x2+a3x3+o(x3)],
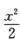 +o(x3)=[1-x+
+o(x3)=[1-x+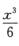 +o(x3)][a1x+a2x2+a3x3+o(x3)],
+o(x3)][a1x+a2x2+a3x3+o(x3)],
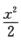 +o(x3)=a1x+(a2-a1)x2+(a3-a2)x3+o(x3),
+o(x3)=a1x+(a2-a1)x2+(a3-a2)x3+o(x3),
比较两端各项系数,得a1=0,a2-a1=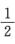 ,a3-a2=0,求得a1=0,a3=a2=
,a3-a2=0,求得a1=0,a3=a2=本文档预览:3000字符,共12317字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载