考研数学三（极限与连续）模拟试卷7

考研数学三（极限与连续）模拟试卷7

选择题

1.设g(x)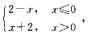＝，f(x)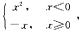＝则g[f(x)]＝________．

(D)

A.

B.

C.

D.

解析：g[f(x)]＝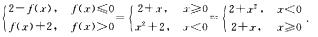

2.函数y＝(B)

A. [－1，1]

B. C. [0，1]

D. [－1／2，1／2]

解析：

3.当x→0时，变量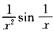(D)

A. 无穷小

B. 无穷大

C. 有界的，但不是无穷小量

D. 无界的，但不是无穷大

解析：取x_k＝1／2kπ，则f(x_k)＝(2kπ)²sin(2kπ)＝0．故x→0时，f(x)不是无穷大，排除B．

显然，x→0时，(1／x²)sin(1／x)不是无穷小，排除A．

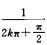取x_k＝，则x_k＝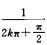

4.当x→0时，下列4个无穷小量中比其他3个更高阶的无穷小量是________．(C)

A. ln(1＋x)

B. e^x－1

C. tanx－sinx

D. 1－cosx

解析：因为x→0时，ln(1＋x)～x，e^x－1～x，1－cosx～x²／2，tanx－sinx～x³／2．

故应选C．

5.设函数f(x)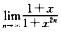＝(B)

A. 不存在间断点

B. 存在间断点x＝1

C. 存在间断点x＝0

D. 存在间断点x＝－1

解析：当|x|＜1时，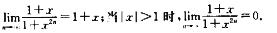

故f(x)＝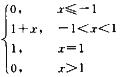

由于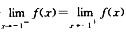＝f(－1)＝0.所以x＝－1为连续点.而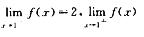

6.设f(x)和φ(x)在(－∞，＋∞)内有定义，f(x)为连续函数，且f(x)≠0，φ(x)有间断点，则(D)

A. φ[f(x)]必有间断点

B. [φ(x)]²必有间断点

C. f[φ(x)]必有间断点

D. φ(x)／f(x)必有间断点

解析：采用排除法，若取φ(x)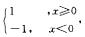＝φ(x)有间断点x＝0.但[φ(x)]²＝1没有间断点，所以B不正确；取φ(x)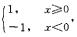＝，f(x)＝x² ，则φ[f(x)]＝1没有间断点，A不正确；取f(x)＝x²，φ(x)＝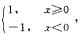

填空题

7.已知f(x)＝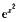

[*]

解析：因为f(x)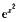＝，所以f[φ(x)]＝本文档预览：3000字符，共7836字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载