考研数学一（函数、极限、连续）模拟试卷55

考研数学一（函数、极限、连续）模拟试卷55

选择题

1.下列函数中非奇非偶的函数是________．(B)

A. f(x)＝3^x－3^－x

B. f(x)＝x(1－x)

C. f(x)＝ln((x＋1)／(x－1))

D. f(x)＝x²cosx

解析：易验证A为奇函数，B为非奇非偶函数，C)为奇函数，D为偶函数．故应选B．

2.设对任意的x，总有φ(x)≤f(x)＜g(x)，且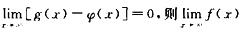(D)

A. 存在且等于零

B. 存在但不一定为零

C. 一定不存在

D. 不一定存在

解析：若取φ(x)＝x，f(x)＝x＋e^－｜x｜，g(x)＝x＋2e^－｜x｜．此时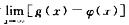＝0.

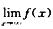但不存在；

若取φ(x)＝0，f(x)＝e^－｜x｜，g(x)＝2e^－｜x｜，此时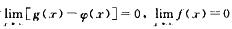

3.函数f(x)＝xsinx________．(C)

A. 当x→∞时为无穷大

B. 在(－∞，＋∞)内有界

C. 在(－∞，＋∞)内无界

D. 当x→∞时有有限极限

解析：只要正确理解当x→∞时，f(x)为无穷大与f(x)无界两个概念之间的区别，就容易作出正确选择．

验证法

可直接验算C为正确选项，根x→∞时f(x)无界的定义，无论给定M多么大，均存在x₀使得f(x₀)＞M．现取正整数k，使(2k＋1／2)π＞M，并令x₀＝(2k＋1／2)π，则f(x₀)＝(2k＋1／2)xsin[(2k＋1／2)π]＝(2k＋1／2)π＞M．

排除法

若取x_k＝2kπ，则f(x_k)＝2kπsin2kπ＝0，故x→∞时，f(x)不是无穷大量．从而排除@A@．分别取x_k⁽¹⁾＝2kπ，x_k⁽²⁾＝(2k＋1／2)π，则当k→∞时f(x_k⁽¹⁾)＝0，而f(x_k⁽²⁾)→∞)，因此，x→∞时f(x)不存在有限极限，且在(－∞，＋∞)内f(x)也不是有界的，于是B、D不成立．

故应选C．

4.设函数f(x)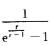＝(D)

A. x＝0，x＝1都是f(x)的第一类间断点.

B. x＝0，x＝1都是f(x)的第二类间断点

C. x＝0是f(x)的第一类间断点，x＝1是f(x)的第二类间断点

D. x＝0是f(x)的第二类间断点，x＝1是(x)的第一类间断点

解析：由于函数f(x)在x＝0，x＝1处无定义，因此是间断点.又因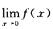＝∞，所以x＝0为第二类间断点:而

5.函数f(x)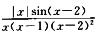＝(A)

A. (－1，0)

B. (0，1)

C. (1，2)

D. (2，3)

解析：x≠0，1，2时，f(x)连续，而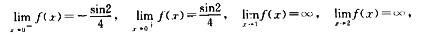

6.设f(x)在(－∞，十∞)内有定义，且(D)

A. x＝0必是g(x)的第一类间断点

B. x＝0必是g(x)的第二类间断点

C. x＝0必是g(x)的连续点

D. g(x)在点x＝0处的连续性与a的取值有关

解析：若a＝0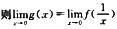，＝0＝g(0)，从而g(x)在x＝0处连续；若a≠0，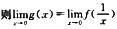

填空题

7.已知函数f(log_ax)＝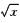

a^x／2，(－∞，＋∞)

解析：令log_ax＝t，则x＝a^t．函数f(log_ax)＝本文档预览：3000字符，共8154字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载