考研数学三（定积分）模拟试卷7

考研数学三（定积分）模拟试卷7

选择题

1.设(x)有连续的导数，f(0)＝0，f’(0)≠0，F(x)＝∫₀^x(x²－t²)f(t)dt，且当x→0时，F’(x)与x^k是同阶无穷小，则k＝________.(C)

A. 1

B. 2.

C. 3

D. 4

解析：F(x)＝x²∫₀^x f(t)dt －∫₀^xt²f(t)dt，则

F’(x)＝2x∫₀^xf(t)dt＋x²f(x)－x²f(x)＝2x∫₀^xf(t)dt.

2.∫₁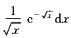^＋∞(A)

A. 2／e

B. －2／e

C. 2e

D. －2e

解析：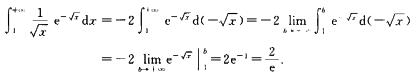

3.下列广义积分发散的是________．

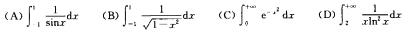(A)

A.

B.

C.

D.

解析：因为∫_－1¹dx发散，且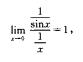

4.设f(x)是连续函数.F(x)是f(x)的原函数，则.(A)

A. 当f(x)是奇函数时，F(x)必是偶函数.

B. 当f(x)是偶函数时，F(x)必是奇函数.

C. 当f(x)是周期函数时，F(x)必是咼期函数.

D. 当f(x)是单调增函数时，F(x)必是单调增函数.

解析：设F(x)＝∫_a^x f(t)dt＝∫₀^xf(t)dt＋C，C为任意常数.

若f(x)为奇函数，则有f(－x)＝－f(x).

F(－x)＝∫₀^－xf(t)dt＋C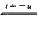

填空题

5.若f(x)＝1／(1＋x²)＋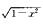

π／(4－π)

解析：记∫₀¹f(x)dx＝I，则π／(4－π)

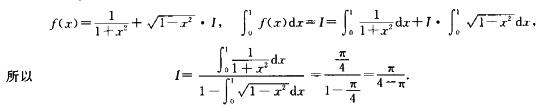
6.

[*]

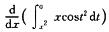
解析：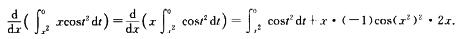

故应填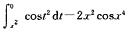

7.设f(x)有一个原函数sinx／x，则∫_0π／2^πxf’(x)dx＝________．

4／π－1

解析：因为(x)有一个原函数sinx／x，所以f(x)＝(sinx／x)’＝(xcosx－sinx)／x²

∫_π／2^πxf ’(x)dx＝∫_π／2^πxdf(x)＝xf(x)|∫_π／2^π－∫_π／2^πf(x)dx

＝(cosx－sinx／x)|∫_π／2^π－(sinx／x)|∫_π／2^π＝4／π－1.

故应填4／π－1.

8.∫₀^＋∞dx／(x²＋4x＋8)＝________．

π／8

解析：原式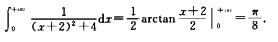

解答题

9.求下列定积分:

(1)∫_－2²max(x，x²)dx；

(2)∫_－3²min(2，x²)dx.

(1)因为max(x，x²)＝[*]

于是

∫_0－2^{2本文档预览：3000字符，共8504字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载}