考研数学一（定积分）模拟试卷16

考研数学一（定积分）模拟试卷16

选择题

1.设f(x)为连续函数，且F(x)＝∫_1／x^lnxf(t)dt，则F’(x)＝________．(A)

A. f(lnx)／x＋f(1／x)／x²

B. f(lnx)＋f(1／x)

C. f(lnx)／x－f(1／x)／x²

D. f(lnx)－f(1／x)

解析：F’(x)＝f(lnx).(1／x)－f(1／x)．(－1／x²)．

故应选A.

2.设f(x)，φ(x)在点x＝0的某邻域内连续，且当x→0时，f(x)是φ(x)的高阶无穷小，则当x→0时，∫₀^xf(t)sintdt是∫₀^xtφ(t)dt的(B)

A. 低阶无穷小

B. 高阶无穷小.

C. 同阶但非等价无穷小

D. 等价无穷小

解析：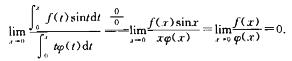

3.若I＝(1／s)∫₀^stf(t＋x／s)dx(s＞0，t＞0)，则I之值________．(C)

A. 依赖于s，t，x

B. 依赖于t和s

C. 依赖于t，不依赖于s

D. 依赖于s，x

解析：利用定积分换元法可推知，I的值与s无关.事实上，I＝(1／s)∫₀^stf(t＋x／s)dx

4.下列广义积分收敛的是________．

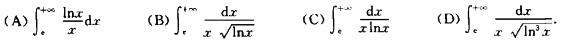(D)

A.

B.

C.

D.

解析：∫_e^＋∞(lnx／x)dx＝∫ _e ^＋∞lnxdlnx＝(1／2)ln²x |∫_e^＋∞， 而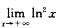不存在.故选项A中积分发散.

同样，由于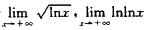均不存在，则B和C中的积分均发散.而

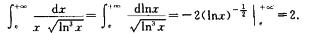
5.(B)

A. ∫₁²ln²xdx

B. 2∫₁²lnxdx

C. 2∫₁²ln(1＋x)dx

D. ∫₁²ln²(1＋x)dx

解析：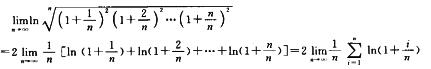

6.设函数f(x)连续，则下列函数中，必为偶函数的是________．(D)

A. ∫₀^xf(t²)dt

B. ∫₀^xf(t)dt

C. ∫₀^xt[f(t)－f(－t)]dt

D. ∫₀^xt[f(t)＋f(－t)]dt

解析：设F(x)＝∫₀^xt[f(t)＋f(－t)]dt，则

F(－x)＝∫₀^－xt[f(t)＋f(－t)]dt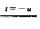

填空题

7.∫₂^＋∞

π／3

解析：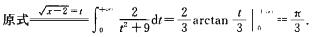

解答题

8.证明:1／2≤∫_π／4^π／2dx≤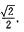

设f(x)＝sinx／x，在[π／4，π／2]上，由cosx＞0，x²＞0，tanx＞x，可得知f’(x)＝(xcosx－sinx)／x²＝cosx(x－tanx)／x²＜0.

故f(x)在[π／4，π／2]上是单调递碱函数，于是有f(π／2)≤f(x)≤f(π／4).又m＝f(π／2)＝2／π，M＝f(π／4)＝[*]

根据定积分的估值定理，有

m(

本文档预览：3000字符，共10551字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载