考研数学二（定积分）模拟试卷5

考研数学二（定积分）模拟试卷5

选择题

1.下列积分中可直接用牛顿—莱布尼慈公式计算的是

(A)

A.

B.

C.

D.

解析：A中的被积函数x／(x²＋1)在[0，5]上连续，且有原函数ln(x²＋1)／2，故可直接应用牛顿—菜布尼兹公式；B中的函数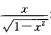

2.设g(x)＝∫₀^xf(u)du，其中f(x)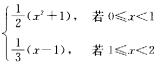＝(D)

A. 无界

B. 递减

C. 不连续

D. 连续

解析：0≤x＜1时，g(x)＝∫₀^x(u²＋1)／2du＝

x³／2＋x)／2，

1＜x＜2时，g(x)＝∫₀¹ (u²＋1)／2du＋∫₁^x(u－1)／3du＝(x²／2－x)／3＋5／6，

故g(x)＝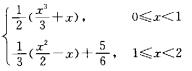

由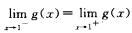

3.把x→0^＋时的无穷小最α＝∫₀^xcost²dt，β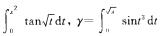＝(B)

A. α，β，γ

B. α，γ，β

C. β，α，γ

D. β，γ，α

解析：

4.设∫₁^xf(t)dt＝x⁴／2－1／2，则∫₁⁴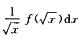(D)

A. 2

B. 7

C. 12

D. 15

解析：因为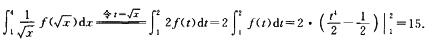

填空题

5.∫_－1¹(|x|＋x)e^－|x|dx＝________.

2(1－2e^－1)

解析：∫_－1¹(|x|－x)e^－|x|dx＝∫_－1¹|x| e^－|x|dx＋∫_－1¹xe^－|x|dx＝∫_－1¹|x| e^－|x|dx

＝2∫₀¹xe^－x＝－2∫₀¹xe^－xdx＝2[∫₀¹xede^－x＝－2[xe^－x｜₀¹－∫₀¹e^－xdx]＝2(1－2e^－1).

故应填2(1－2e^－1).

6.设F(x)＝∫₁^x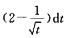

(0，1／4)

解析：F’(x)＝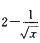

7.广义积分∫₀^＋∞xdx／(1＋x²)²＝________．

1／2

解析：因为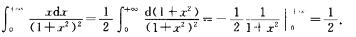

8.已知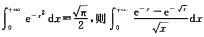

[*]

解析：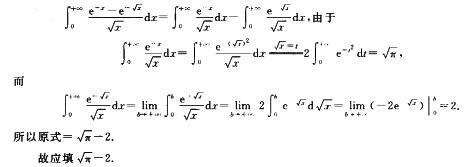

9.设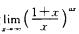

本文档预览：3000字符，共10595字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载