考研数学一（多元函数微分学）模拟试卷40

考研数学一（多元函数微分学）模拟试卷40

选择题

1.函数f(x，y)在点(x₀，y₀ )处偏导数存在，是(x，y)在该点处(C)

A. 连续的充分条件

B. 连续的必要条件

C. 可微的必要条件

D. 可微的充分条件

解析：A不正确，例如函数

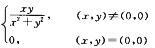
显然有f’_x(0，0)＝f ’_y(0，0)＝0，但(x，y)在点(0.0)处不连续.B不正确，例如函数f(x，y)＝|xy|在点(0，1)处连续，但偏导数f’_x(0，1)不存在.D不正确.例如函数

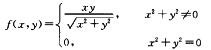
在点(0，0)处有f’_x(0，0)＝0及f’_y(0，0)＝0，但f(x，y)在点(0，0)处不可微；

若函数z＝f(x，y)在点(x，y)处可微，则函数z＝f(x，y)在点(x，y)的偏导数必存在，且dz＝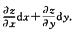

2.考虑二元函数f(x，y)的下面4条性质：

①f(x，y)在点(x₀，y₀)处连续，

②f(x，y)在点(x₀，y₀)处的两个偏导数连续.

③f(x，y)在点(x₀，y₀)处可微，④ f(x，y)在点(x₀，y₀)处的两个偏导数存在，

若用“P→Q”表示可由性质P推出性质Q.则有________.(A)

A. ②→③→①

B. ③→②→①

C. ③→④→①

D. ③→①→④

解析：根据二元函数的连续、偏导数存在及可微之间的关系知选项A正确.

故应选A.

填空题

3.设u＝e^－xsin(x／y)，则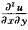

(π／e)²

解析：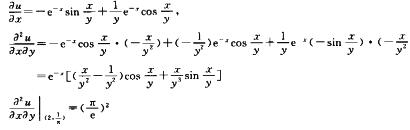

4.设二元函数z＝xe^x＋y＋(x＋1)ln(1＋y).则dz｜_(1，0)＝________．

2edx＋(e＋2)dy

解析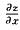：＝e^x＋y＋xe^x＋y＋ln(1＋y)，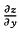

5.设u＝arcsin(z／(x＋y))则du＝________.

[*]

解析：

6.设函数f(u)可微，且f’(0)＝1／2，则x＝f(4x²－y ²)在点(1，2)处的全微分dz|_(1，2)＝________．

4dx－2dy

解析：因为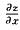＝f’(4x²－y²)．8x，

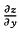＝f’ (4x²－y²).(－2y)，

所以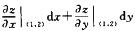

7.设z＝e^－x－f(x－2y)，且当 y＝0时，z＝x²，则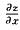

2(x－2y)－e^－x＋e^－x＋2y

解析：把y＝0时，z＝x²代入函数表达式得

x²＝e^－x－f(x)，即f(x)＝e^－x－x²，

从面z＝e^－x－e^－x＋2y＋(x－2y)²，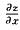

8.设z＝xyf(y／x)，f(u)可导，则xz_x＋yz_y＝________.

本文档预览：3000字符，共8919字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载