考研数学二（重积分）模拟试卷25

考研数学二（重积分）模拟试卷25

选择题

1.设f(x，y)是连续函数，则∫₀^adx∫₀^xf(x，y)dy(B)

A. ∫₀^ady∫₀^yf(x，y)dx

B. ∫₀^ady∫_y^af(x，y)dx

C. ∫₀^ady∫₀^yf(x，y)dx

D. ∫₀^ady∫₀^af(x，y)dx

解析：改换二次积分的积分次序以及确定积分上下限的技巧和方法，解题关键是先由所给的二次积分的积分限确定积分区域D(本题积分区域为x轴，y＝x以及x＝a确定的三角形区域)，然后再化为先对x积分后对y积分的二次积分.

故应选B.

2.设有闭区域Ω₁：x²＋y²＋z²≤R²，z≥0； Ω₂：x²＋y²＋z²≤R²，x≥0，y≥0，z≥0.则

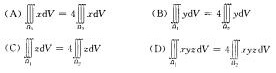(C)

A.

B.

C.

D.

解析：因为区域Ω₁既关于xOz面对称，又关于yOz面对称，区城Ω₂恰是Ω₁的1／4，但被积函数

数中只有f(x，y，z)＝z是既关于xOy面、又关于yOz面对称.

故应选C.

填空题

3.积分∫₀²dx∫_x²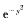

(1－e^－4)／2

解析：由于被积函数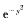的原函数不能用初等函数表示.所以应改变二次积分的积分次序，故

∫₀²dx∫_x²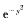dy＝∫₀²dy∫₀^y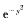dx＝∫₀²y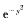

4.设∑为球面x²＋y²＋z²＝9的外侧面，则曲面积分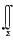

36π

解析：当积分曲面是封闭曲面时，对坐标的曲面积分一般应用高斯公式计算，设几是由闭曲面∑所围的球体，则

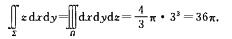
解答题

5.计算二重积分

[*]

解析：

6.计算二重积分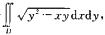

如图所示.

[*]

解析：

7.计算积分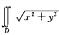

利用极坐标，则

[*]

解析：

8.计算二重积分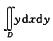，其中D是由直线上x＝－2，y＝0，y＝2以及曲线x＝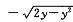

区域D和D₁如图所示，有

[*]

在极坐标系下，有D₁={(r，θ)|π／2≤0≤r，θ≤r≤2sinθ}，因此

[*]

解析：

9.

[*]

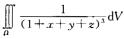
解析：

10.计算本文档预览：3000字符，共8127字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载