考研数学二（重积分）模拟试卷23

考研数学二（重积分）模拟试卷23

选择题

1.设f(x，y)连续，且f(x，y)＝xy＋(C)

A. xy

B. 2xy

C. xy＋1／8

D. xy＋1

解析：记f(u，v)dudv＝1，则f(x，y)＝xy＋I

等式两端同时取二重积分得

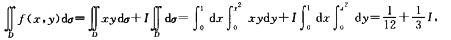
2.设函数f(u)连续，区城D＝{(x，y)|x²＋y²≤2y} ，则f(xy)dxdy＝________.

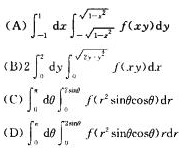(D)

A.

B.

C.

D.

解析：在直角坐标系下

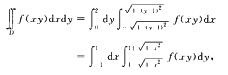
故应排除A、B.

在极坐标系下，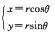

[f(x，y)dxdy＝∫₀^xdθ∫₀^2sinθf(r²sinθcosθ)rdr

3.设区城D＝{(x，y)|x²＋y²≤4，x≥0，y≥0}，/(x)f(x)为D上的正值连续函数，a，b为常数，则 (D)

A. abπ

B. abπ／2

C. (a＋b)π

D. (a＋b)π／2

解析：因D：x²＋y²≤4，x≥0.y≥0，对 x，y具有轮换对称性，故

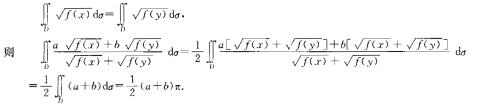
4.设Ω由z＝x²＋y²与z＝1所围区域在第一卦限的部分，则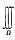f(x，y，z)dV≠________．

(B)

A.

B.

C.

D.

解析：因为关于z的积分上下限分别为1和x²＋y ².

故应选B.

填空题

5.设a＞0，f(x)＝g(x)＝而D表示全平面，则I＝

a²

解析：

6.设曲面∑是z＝(x²＋y²)／2被平面z＝2所截下的有限部分，则曲面积分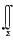

[*]

解析：设∑在xOy 平面上投影为D_xy，即

D_xy：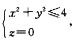

由z＝(x²＋y²)有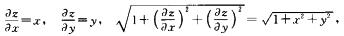

所以

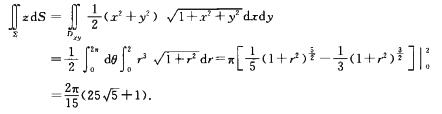
故应填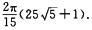

解答题

7.计算本文档预览：3000字符，共10251字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载