考研数学一（向量代数与空间解析几何）模拟试卷16

考研数学一（向量代数与空间解析几何）模拟试卷16

选择题

1.设有直线L₁(x－1)／1＝(y－5)／(－2)＝(z＋8)／1与L₂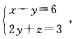：(C)

A. π／6

B. π／4

C. π／3

D. π／2

解析：s₁＝{1，－2，1}，s₂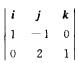＝＝{－1，－1，2}，则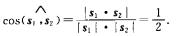

2.设有直线L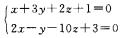：(C)

A. 平行于π

B. 在π上

C. 垂直于π

D. 与π斜交

解析：直线L的方向向量为s＝(－28，14，－7).平面π的法向向量为n＝{4，－2，1)，由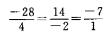

填空题

3.点(2，1，0)到平面3x＋4y＋5z＝0的距离d＝_____.

[*]

解析：d＝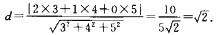

故应填

4.已知两条真线的方程是.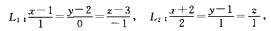

x－3y＋z＋2＝0

解析：根据题意，所求平面应过直线L₁，从而过直线L₁上的点(1，2，3)，另一方面所求平面的法向量n与已知直线L₁及L₂的方向向量都垂直，从而可取

n＝

解答题

5.求与已如直线L₁：(x＋3)／2＝(y－5)／1＝z／1和L₂：(x－3)／1＝(y＋1)／4＝z／1都相交.且与L₃：(x＋2)／3＝(y－1)／2＝(z－3)／1平行的直线方程．

将L₁和L₂化为参数方程：[*]

设L与L₁和L₂的交点分别对应参数t₁和t₂，则知交点分别为

P(2t₁－3，t₁＋5，t₁)，Q(t₂＋3，4t₂－1，t₂).

由于[*]，故[*]

整理成方程组[*]解出t₁＝0.所以P的坐标为(－3，5，0).故所求直线方程为： (x＋3)／3＝(y－5)／2＝z／1．

解析：

6.求点P(3，－1，2)到直线L：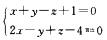

直线方程L 的对称式方程为(x－1)／0＝(y＋2)／1＝(z－0)／1，过点P且垂直于直线L的平面π的方程为0．(x－3)＋1. (y＋1)＋1. (z－2)＝0， 即y＋z－1＝0.

把直线L的参数方程[*]

代入平面π方程，求直线L与平面π的交点－2＋t＋t－1＝0→t＝3／2，交点为M(－1／2，3／2)

[*]

解析：

7.求点P(1，2，－1)到直线L：(x－1)／2＝(y＋1)／(－1)＝(z－2)／3的距离.

解法一

过点 P(1，2，－1)且垂直于直线L的平面的方程为

2(x－1)－(y－2)＋3(z＋1)＝0，

即2x－y＋3z＋3＝0.

该平面与直线L.相交于点Q(－5／7，－1／7，－4／7)，所以，所求的距离

[*]

解法二

直线 L的方向向量是s＝{2，－1，3}.而点P₀(1，－1，2)在直线L上，所以，点P(1，2.，－1)到直线L的距离为

[*]

如图所示.

[*]

而

[*]

解析：

请指出下列二次曲面的名称，并作草图：

8.16x²－9y²－9z²＝－25；

可以将方程写成如下的标准形式：

[*]

该方程表示单叶双曲面，如图所示：

[*]

解析：

9.16x²－9y²－9z²＝25；

方程可以写成如下的标准形式：

[*]

该方程表示双叶双曲面，如图所示：

[*]

解析：

10.y²＋z²＝4x；

程可以写成如下的标准形式：

本文档预览：3000字符，共10992字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载