考研数学一（向量代数与空间解析几何）模拟试卷15
选择题
1.下列等式正确的是________．(C)
A. |a|a＝a2
B. a. (b．b)＝－ab2
C. a．b＝b. a
D. a×b＝b×a
解析：选项A错误：因a2＝a． a＝|a|2；
选项B错误：因a. (b. b)无意义；
选项D错误：因a×b＝－b×a；
选项C正确：因a. b＝|a|．|b|．
2.已知a，b均为非零向量，而|a＋b|＝|a－b|.则(C)
A. a－b＝0
B. a＋b＝0
C. a. b＝0
D. a×b＝0
解析：由a≠0，b≠0及|a＋b|＝|a－b|知
(a＋b)．(a＋b)＝(a－b)．(a－b)即2a. b＝－2a．b.
所以a. b＝0.
故应选C.
填空题
3.已知a、b、c都是单位向量，且满足a＋b＋c＝0，则a．b＋b．c＋c．a＝________．
－3／2
解析：利用数量积的运算规律和单位向量的概念求解
0＝(a＋b＋c)．(a＋b＋c)＝a．a＋b. b＋c．c＋2(a．b＋b. c＋c．a)
＝3＋2(a. b＋b. c＋c. a)．
于是a. b＋b. c＋c. a＝－3／2．
故应填－3／2．
4.已知|a|＝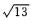
， |b|＝
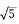，|c|＝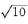
－7
解析：由a＋b＋c＝{3，1，－2}知|a＋b＋c|2＝(a＋b＋c)2＝14.另一方面
(a＋b＋c)2＝(a＋b＋c)．(a＋b＋c)＝|a|2＋|b|2＋|c|2＋2(a. b＋b. c＋c. a)
＝28＋2(a. b＋b. c＋c. a)，
所以a. b＋b. c＋c. a＝(14－28)／2＝－7.
故应填－7.
5.已知向量a＝a，i＋3j＋4k，b＝4i＋a，j－7k，则当ax＝________时，a垂直于b.
4
解析：a⊥b，a．b＝0，4ax＋3ax-－28＝0.
所以ax＝4. .
故应填4.
6.设向量x与向量a＝2i－j＋3k平行.且满足方程a. x＝7，则向量x＝________.
i－j／2＋3k／2
解析：设x＝{x1，x2，x3)，由x//a得x1／2＝x2／－1＝x3／3，由a.x＝7，得2x1－x2＋3x3＝7，解得
x1＝1，x2＝－1／2，x3＝3／2．
所以x＝i－j／2＋3k／2.
故应填i－j／2＋3k／2.
7.设(a×b)．c＝2，则[(a＋b)×(b＋c)]．(c＋a)＝________.
4
解析：原式＝[a×b＋a×c＋b×c]．(c＋a)
＝(a×b)．c＋(a×c)．c＋(b×c)．c＋(a×b)．a＋(a×c)．a＋(b×c)．a
＝(a×b)．c＋(b×c)．a＝2(a×b)．c＝4.
故应填4.
8.以向量a＝m＋2n和b＝m－3n为边的三角形的面积为________，其中 |m|＝5，|n|＝3，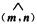
75／4
解析：设三角形面积为A.则 A＝｜a×b｜／2，而
A×b＝(m＋2n)×(m－3n)＝m×m－3m×n＋2n×m－6n×n
＝0＋3m×m＋2n×m－0＝5n×m，
因此A＝|a×b|／2＝2|n×m|／5＝(5／2)．|n|．|m|sin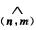
9.过三个点P(2，3，0)，Q(－2，－3，4) ，R(0，6，0)的平面方程是________．
3x＋2y＋6z－12＝0
解析：设该平面的方程为 Ax＋By＋Cz＋D＝0，则因点P，Q，R在此平面上，故有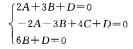
10.过点M0(2，4，0)且与直线L：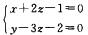
(x－2)／(－2)＝(y－4)／3＝z／1
解析：直线L的方向向量为
s＝本文档预览：3000字符，共9377字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
