考研数学二（重积分）模拟试卷28

考研数学二（重积分）模拟试卷28

选择题

1.下列四个等式中不成立的是________．其中D：x²＋y²≤1，D₁：x2²＋y²≤1，x≥0， y≥0.

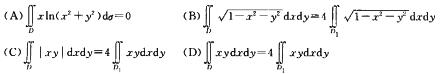(D )

A. 等式是正确的. 因为积分区域对称于y轴，被积函数关于x是奇函数，将该二重积分化为累次积分，且首先对x积分时，将是奇函数在对称的积分区间上的积分，故积分值为零．

B. 等式是成立的，因为积分区域D)对称于x轴和y轴，被积函数只出现x及y的平方项，其图形对称于xOz及yOz平面，故D上的积分可以用D₁上积分的4倍来表示(上述等式的几何意义是：中心在原点的上半球，等于它的第一卦限部分的4倍).

C. 等式是成立的，因为这时被积函数f(x，y)＝|xy|也对称于xOz和yOz平面.

D. 等式不成立.积分区城D虽仍然对称于x轴，y轴，但被积函数对x，y均为奇函数，其在一、三象限是正的，二、四象限是负的，故D上的积分不能为D₁上积分的4倍，而是0(被积函数f(x，y)＝xy的几何图形是一个马鞍面)．

解析：A等式是正确的. 因为积分区域对称于y轴，被积函数关于x是奇函数，将该二重积分化为累次积分，且首先对x积分时，将是奇函数在对称的积分区间上的积分，故积分值为零．B等式是成立的，因为积分区域D)对称于x轴和y轴，被积函数只出现x及y的平方项，其图形对称于xOz及yOz平面，故D上的积分可以用D₁上积分的4倍来表示(上述等式的几何意义是：中心在原点的上半球，等于它的第一卦限部分的4倍).C等式是成立的，因为这时被积函数f(x，y)＝|xy|也对称于xOz和yOz平面.D等式不成立.积分区城D虽仍然对称于x轴，y轴，但被积函数对x，y均为奇函数，其在一、三象限是正的，二、四象限是负的，故D上的积分不能为D₁上积分的4倍，而是0(被积函数f(x，y)＝xy的几何图形是一个马鞍面)．

故应选D.

2.设曲线积分∫_L[f(x)－e^x]sinydx－f(x)cosydy与路径无关，其中f(x)具有一阶连续导数，且f(0)＝0，则f(x)＝________.(B)

A. (e^－x－e^x)／2

B. (e^x－e^－x)／2

C. (e^x＋e^－x)／2－1

D. 1－(e^x－e^－x)／2

解析：P＝[f(x)-e^x]siny，Q＝－f(x)cosy

由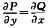

填空题

3.交换二次积分的积分次序：∫_－1⁰dy ∫₂^1－yf(x，y)dx＝________.

∫₁²dx∫₀^1－x f(x，y)dy

解析：∫_－1⁰∫₂^1－yf(x，y)dx＝－∫_－1⁰dy∫_1－y²f(x，y)dx，

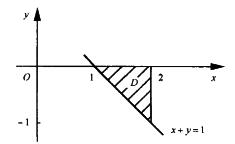
积分区域D为

D＝{(x，y)｜－1≤y≤0， 1－y≤x≤2}.

如图所示.

4.设Ω为x²＋y²＋(z－1)²≤1.则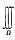

－4π

解析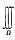：(x＋xyz²－3)dV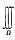＝x(1＋yz²)dV－3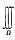dV＝I₁＋I₂.

对于I₁，由于被积函数x(1＋yz²)关于x为奇函数，而积分区域关于yOz面对称，所以I₁＝0；而I₂＝－3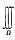

5.设平面曲线L为下半圆周y＝－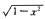

π

解析：由于在L上x²＋y²＝1，所以

∫_L(x²＋y²)ds＝∫_Lds＝π．

6.设∑是圆柱面x²＋y²＝1与平面z＝0，z＝3所围成的封闭曲面的外侧，则曲面积分本文档预览：3000字符，共9299字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载