考研数学二（多元函数微分学）模拟试卷58

考研数学二（多元函数微分学）模拟试卷58

选择题

1.设f(x，y)与φ(x，y)均为可微函数，且φ’_y(x，y)≠0.已知(x₀，y₀)是f(x，y)在约束，条件φ(x，y)＝0下的一个极值点，下列选项正确的是________.(D)

A. 若f’_x(x₀，y₀)＝0，则 f’_y(x₀，y₀)＝0

B. 若f’_x(x₀，y₀)＝0.则f’_y(x₀，y₀)≠0

C. 若f’_x(x₀，y₀)≠0，则f’_y(x₀，y₀)＝0

D. 若f’_x(x₀，y₀)≠0，则f’_y(x₀，y₀)≠0

解析：设F(x，y)＝f(x，y)＋λφ(x，y)，由题设知

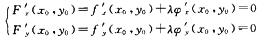
2.设函数z＝f(x，y).有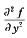(B)

A. 1－xy＋y²

B. 1＋xy＋y²

C. 1－x²y＋y²

D. 1＋x²y＋y²

解析：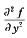

3.设z(x，y)＝(1－y²)f(y－2x).，且已知f’(y)＝ye^x／(1＋y)²，f(0)，1.则∫₀²z(1，y)dy＝________.(B)

A. －1

B. －2

C. 1

D. 2

解析：由f’(y)＝ye^x／(1＋y)²，有

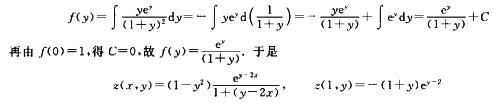
填空题

4.函数f(u，v)由关系式f[xg(y)，y]＝x＋g(y)确定，其中函数g(y)可微，且g(y)≠0，则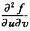

[*]

解析：由f[xg(y)，y]＝x＋g(y)得f(u，v)＝u／g(v)＋g(v)，

5.设函数f(x，y，z)＝e^xyz²，其中z＝z(x，y)是由x＋y＋z＋xyz＝0确定的隐函数，则f’_x(0，1，－1)＝________.

1

解析：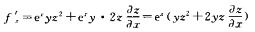

由x＋y＋z＋xyz＝0，两边关于x求导得

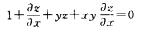
把(0，1，－1)代入得，

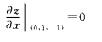
解答题

6.求函数z＝3axy－x³－y³(a＞0)的极值.

解方程组[*]

解得驻点：(0，0)，(a，a).又[*]

于是在点(0，0)处有

A＝0，B＝3a， C＝0，AC－B²＝－9a²＜0

故(0，0)不是函数的极值点

又在点(a，a)处有

A＝－6a，B＝3a，C＝6a， AC－B²＝27a²＞0

又A＝－6a＜0，故所给函数在(a，a)处有极大值z_max＝a³.

解析：

7.某养殖场饲养两种鱼，若甲种鱼放养x(万尾)，乙种鱼放养y(万尾)，收获时两种鱼的收获量分别为(3－αx－βy)x和(4－βx－2αy)y (α＞β＞0)，求使产鱼总量最大的放养数.

设产鱼总量为z，则

z＝3x＋4y－αx²－2αy²－2βxy

由极值的必要条件，得方程组[*]

由于α＞β＞0.知其系数行列式△＝4(2α²－β²)＞0.故方程组有唯一解

[*]

有

B²－AC＝4β²－8α²＝－4(2α²－β²)

由条件知B²－AC＜0，且A＜0，因此z在(x₀，y₀

本文档预览：3000字符，共10778字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载