考研数学一（定积分的应用）模拟试卷5

考研数学一（定积分的应用）模拟试卷5

选择题

1.设f(x)，g(x)在区间[a，b]上连续，且g(x)＜f(x)＜m(m为常数).则曲线y＝g(x)，y＝f(x).x＝a及x＝b所围平面图形绕直线y＝m旋转而成的旋转体体积为(B)

A. ∫_a^bπ[2m－f(x)＋g(r)][f(x)－g(x)]dx

B. ∫_a^b π[2m－f(x)－g(x)][f(x)－g(x)]dx

C. ∫_a^bπ[m－f(x)＋g(x)][f(x)－g(x)]dx

D. ∫_a^b π[m－f(x)－g(x)][f(x)－g(x)]dx

解析：本题可以看成曲边梯形

{(x，y)| f(x)≤y≤m，a≤x≤b}

与曲边梯形

{(x，y)|g(x)≤y≤m，a≤x≤b}

分别绕y＝m旋转所得体积的差，即

V＝π∫_a^b[m－pg(x)]²dx－π∫_a^b [m－f(x)]²dx

＝∫_a^bπ([2m－f(x)－g(x)][f(x)－g(x)]dx.

故应选B.

解答题

2.设星形线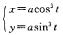

如图所示.

[*]

在弧上取一小段ds，将其近似地看成质点(x，y)，其质量为(x²＋y²)^3／2ds.由两质点间的引力计算公式，此小段对在原点处的单位质点的引力dF的大小为

[*]

(其中k为引力系数)

从而可求出dF在水平方向和垂直的分力分别为

dF_x＝dF．cosα＝k(x²＋y²)^1／2．[*]＝kxds

dF_y＝dF．sinα＝k(x²＋y²)^1／2．[*]＝kyds

从而

F_x＝∫_A^Bkxds＝k∫₀^π／2acos³t [*]＝3a²k∫₀^π／2cos⁴t．cos⁴t. sintdt＝－ 3a²k∫₀^π／2cos⁴td(cost)＝3ka²／5．

F_y＝∫_A^Bkyds＝k ∫₀^π／2asin³t [*]

＝3a²k∫₀^π／2sin⁴t. costdt＝3a²k∫₀^π／2sin⁴td(sint

)＝3ka²／5.

所以星形线在第一象限的弧段对位于原点处的单位质点的引力为

F＝3ka²i／5＋3ka²j／5.

解析：

3.设有质量均匀分布的细杆，线密度为常量p，长为1，在杆的中垂线上：到杆距离为a处有一单位质点M，求杆对这单位质点的引力．

根据万有引力定律，由微元法：

[*]

解析：

一质量为 M.长为l的均匀杆AB吸引着质量为m的一质点C，此质点C位于AB杆的延长线上，并与较近的端点B的距高为a.试求：

4.杆与质点间的相互吸引力；

如图所示.

[*]

据万有引力定律，由微元法有

[*]

其中k为常数．

解析：

5.总质点在杆的延长线上从距离r₁处移至r₂处时，克服吸引力所作的功.

位于B.C间距B端为工的点与杆AB的引力为F＝kmM／x(x＋1)，所以

[*]

解析：

6.设人呼出或吸入的气流的速率v(t)(m/s)，可用一个正弦曲线v(t)＝Asin(2πt／T)来描述，其中时间(单位为秒)从某次吸气开始时计算起，A是最大气流速率，T为一次呼吸所用时间，当正弦曲线函数值为正时，人正在吸气；反之，正在呼气.在吸气的某个时间段[t₁，t₂]上，曲线y＝v(t)与t＝t₁，t＝t₂及t轴所围面积就是人在这个时间段上吸入空气总量.试求人每次吸气时吸入空气的总量.

人每次吸气时吸入空气总量为 [*]

解析：

7.设xOy平面上有正方形D＝{(x，y)|0≤x≤1，0≤y≤1}及直线l：x＋y＝t (t≥0).若S(t)表示正方形D位于直线1左下方部分的面积，试求∫₀^xS(t)dt (x≥0).

如图所示. 由题设知

[*]

所以，当0≤x≤1时，

∫₀^xS(t)dt＝∫₀^x(t²／2)dt＝x³／6，当1＜x≤2时

∫₀^xS(t)dt＝∫₀¹S(t)dt＋∫₁^xS

本文档预览：3000字符，共9708字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载