2018年下半年中学教师资格认定考试（初级数学学科知识与教学能力）真题试卷
单项选择题
1.与向量a=(2，3，1)垂直的平面是( )。(C。)
A. x一2y+z=3
B. 2x+y+3z=3
C. 2x+3y+z=3
D. x一y+z=3
解析：本题考查空间解析几何中平面的法向量的相关知识。平面的法向量是垂直于平面的非零向量。在直角坐标系中，平面Ax+By+Cz+D=0(A，B，C不同时为零)的一个法向量为n=(A，B，C)。本题中，向量α=(2，3，1)为平面2x+3y+z=3的法向量，故垂直于平面2x+3y+z=3。故本题选C。
2.
(C。)
A. 0
B. 1
C. 3
D. ∞
解析：本题考查函数极限的四则运算以及等价无穷小量替换。
(方法一)当x→0时，tan3x～3x。所以
=3。
(方法二)
3.函数饭f(x)在[a，b]上黎曼可积的必要条件是f(x)在[a，b]上( )。(D。)
A. 可微
B. 连续
C. 不连续点个数有限
D. 有界
解析：本题考查黎曼可积的条件。
若函f(x)在[a，b]上(黎曼)可积，则f(x)在[a，b]上必有界(可积的必要条件)，故本题选D。
下面说明其他三个选项。可积的充分条件有以下3个：①函数在闭区间上连续；②函数在闭区间上有界且只有有限个间断点；③函数在闭区间上单调。由此可排除B项和C项。又因为在一元函数中，可微一定连续，且连续一定可积．但反之不成立．故排除A项。
一元函数在闭区间上连续、可导、可微、可积、有界的关系图如下：
4.定积分
dx(a＞0，b＞0)的值是( )。
(B。)
A.
B.
C.
D.
解析：本题考查定积分的几何意义或定积分的计算。
(方法一)定积分
表示被积函数y=
与x轴所围成的图形的面积，即椭圆
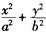在x轴上方部分的面积。而椭圆
=1的面积为πab。所以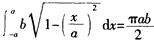
5.与向量α=(1，0，1)，β=(1，1，0)线性相关的向量是( )。(A。)
A. (3，2，1)
B. (1，2，1)
C. (1，2，0)
D. (3，2，2)
解析：(方法一)一个向量组中，若一个向量可由其余向量线性表出，则这几个向量必线性相关；若任意一个向量都不能被其余向量线性表出，则这几个向量必线性无关。结合选项可知，只有选项A可以由向量α和向量β线性表出，即(3，2，1)=α+2β。故本题选A。
(方法二)向量组α，β，γ线性相关
矩阵A=(αT，βT，γT)的秩小于向量的个数∣A∣=0；向量组α，β，γ线性无关矩阵A=(αT，βT，γT)满秩∣A∣≠0。结合选项知，
6.设f(x)=acosx+bsinx是R到R的函数，V={f(x)∣f(x)=acosx+bsinx，a，b∈R}是线性空间，则V的维数是( )。(B。)
A. 1
B. 2
C. 3
D. ∞
解析：本题考查线性空间的维数、线性空间的基。由题意知，线性空间V中的每一个元素都是cosx和sinx的线性组合。而cosx和sinx是线性无关的，这是因为如果存在实数m，n，使得mcosx+nsinx=0对任意x∈R都成立，则m=n=0。因此cosx和sinx是线性空间V的一组基，所以V的维数是2。故本题选B。
7.在下列描述课程目标的行为动词中，要求最高的是( )。(C。)
A. 理解
B. 了解
C. 掌握
D. 知道
解析：本题考查《义务教育数学课程标准(2011年版)》中课程目标行为动词的相关知识。在课程标准中有两类行为动词，一类是描述结果目标的行为动词，包括“了解(知道)、理解、掌握、运用”等术语。另一类是描述过程目标的行为动词，包括“经历、体验、探索”等术语。每一组术语中按照从前到后的顺序要求递增，即行为动词按要求的高低排序为了解(知道)＜理解＜掌握＜运用，经历＜体验＜探索。故本题选C。
8.命题P的逆命题和命题P的否命题的关系是( )。(A。)
A. 同真同假
B. 同真不同假
C. 同假不同真
本文档预览：3000字符，共11714字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
