2019年上半年中学教师资格认定考试（初级数学学科知识与教学能力）真题试卷
单项选择题
1.下列选项中，运算结果一定是无理数的是( )。(A。)
A. 有理数与无理数的和
B. 有理数与有理数的差
C. 无理数与无理数的和
D. 无理数与无理数的差
解析：本题考查有理数与无理数的性质。(1)有理数与有理数：和、差、积、商均为有理数(求商时分母不为零)。(2)有理数与无理数：①一个有理数和一个无理数的和、差为无理数；②一个非零有理数与一个无理数的积、商为无理数。(3)无理数与无理数：和、差、积、商可能是有理数，也可能是无理数。故本题选A。
2.在空间直角坐标系中，由参数方程
(0≤t≤2π)所确定的曲线的一般方程是( )。
(B。)
A.
B.
C.
D.
解析：本题考查空间曲线的方程。由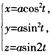
，可得x+y=acos2t+asin2t=a，z2=a2(2sintcost)2=4xy，所以将参数方程化成一般方程为
3.已知空间直角坐标与球坐标的变换公式为
(ρ≥0，－π＜φ≤π，
≤θ≤
，则在球坐标系中，
(D。)
A. 柱面
B. 圆面
C. 半平面
D. 半锥面
解析：本题考查直角坐标与球坐标变换、空间曲面方程。
设球坐标中任意一点P(ρ，θ，φ)，根据题目中空间直角坐标与球坐标的变换公式可知，ρ表示原点O与点P之间的径向距离，θ表示OP＇到OP的有向角，其中OP＇是OP在xOy坐标面上的投影，φ表示Ox轴到OP＇的有向角，如图1所示。因此，
表示以原点为顶点，以射线OP为母线，以z轴为中心轴的半锥面，如图2所示。故本题选D。
4.设A为n阶方阵，B是A经过若干次初等行变换得到的矩阵，则下列结论正确的是( )。(C。)
A. ∣A∣=∣B∣
B. ∣A∣≠∣B∣
C. 若∣A∣=0，则一定有∣B∣=0
D. 若∣A∣＞0，则一定有∣B∣＞0
解析：本题考查矩阵初等变换及行列式的性质。对矩阵可以作如下三种初等行(列)变换：①交换矩阵的两行(列)；②将一个非零数k乘到矩阵的某一行(列)；③将矩阵的某一行(列)的后倍加到另一行(列)上。若方阵A，经过以上三种初等变换得到方阵B，则对应的行列式的关系依次为∣A∣=一∣B∣，∣A∣=k∣B∣，∣A∣=∣B∣。即∣A∣=a∣B∣，a∈R。所以∣A∣=0时必有∣B∣=0。故本题选C。
5.已知f(x)=
(B。)
A. －1
B. 0
C. 1
D. π
解析：本题考查泰勒展式的相关知识。因为sinx=
，所以f(x)=
6.若矩阵
(C。)
A. x=－2，y=2
B. x=1，y=－1
C. x=2，y=－2
D. x=－1，y=1
解析：本题考查矩阵的相似对角化的相关知识。由题意可知，矩阵A可以相似对角化，且λ=2对应两个线性无关的特征向量，所以(2E－A)x=0有两个线性无关的解，即有3一r(2E－A)=2，所以r(2E－A)=1。2E－A=
，要使r(2E－A)=1，则有
7.下列描述为演绎推理的是( )。(A。)
A. 从一般到特殊的推理
B. 从特殊到一般的推理
C. 通过实验验证结论的推理
D. 通过观察猜想得到结论的推理
解析：演绎推理是从一般规律出发，运用逻辑证明或数学运算，得出特殊事物应遵循的规律，即从一般到特殊的推理。归纳推理是由个别、特殊到一般的推理，通过实验验证结论和通过观察猜想得到结论的推理都是归纳推理。故本题选A。
8.《义务教育数学课程标准(2011年版)》从四个方面阐述了课程目标，这四个目标是( )。(A。)
A. 知识技能、数学思考、问题解决、情感态度
B. 基础知识、基本技能、问题解决、情感态度
C. 基础知识、基本技能、数学思考、情感态度
D. 知识技能、问题解决、数学创新、情感态度
解析：《义务教育数学课程标准(2011年版)》指出，义务教育阶段数学课程目标分为总目标和学段目标，从知识技能、数学思考、问题解决、情感态度等四个方面加以阐述。
简答题
一次实践活动中，某班甲、乙两个小组各20名同学在综合实践基地脱玉米粒，一天内每人完成脱粒数量
本文档预览：3000字符，共13375字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
