中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷50

中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷50

单项选择题

1.下列哪个方程表示一条空间直线。( )(D。)

A. x²+y²+z²一2x+4y=0

B. z=x²+y²

C. y=x

D. 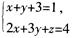解析：A项表示空间的球面；B项表示一个旋转抛物面；C项表示空间中的一个平面；D项表示一条空间直线。故本题选D。

2.设A为n(n≥3)阶方阵，则下列说法正确的是( )。(B。)

A. 如果存在数λ和向量α使得Aα=λα，则α是A的属于特征值λ的特征向量

B. 如果存在数λ和非零向量α使得(λE—A)α=0，则λ是A的特征值

C. A的不同的特征值可以有同一个特征向量

D. A的不同的特征值分别对应的特征向量可能线性相关

解析：如果存在数λ和非零向量α使得Aα=λα，则α是A的属于特征值λ的特征向量，A项错误；根据矩阵特征值的定义，B项正确；矩阵的不同的特征值对应不同的特征向量，且不同的特征值对应的特征向量线性无关，所以C项和D项均错误。故本题选B。

3.下列数列收敛的是( )。

B。

解析：A项中，当n→∞时，{(一1)ⁿ}的极限不存在，该数列发散；B项中，因为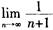=0,所以数列收敛；C项和D项中，因为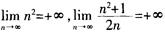，所以数列{n²}和数列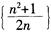

4.设A，B为独立的事件，且P(A)＞0，P(B)＞0，则下面四个式子中不成立的是( )。(C。)

A. P(BIA)＞0

B. P(A∣B)=P(A)

C. P(A∣B)=0

D. P(AB)=P(A)·P(B)

解析：因为A，B为独立的事件，所以P(AB)=P(A)·P(B)，P(B|A)=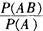=P(B)＞0，P(A|B)=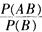

5.下列命题正确的个数是( )。

(1)若f(x)是[a，b]上的连续函数，则f(x)在[a，b]上可导；

(2)若函数f(x)在[a，b]上可导，则f(x)是[a，b]上的连续函数；

(3)“函数f(x)在[a，b]上可导”是“函数f(x)在[a，b]上可微”的充要条件；

(4)若f(x)是(a，b)上的连续函数，则f(x)在(a，b)上可积；

(5)若函数f(x)在[a，b]上有界，且只有有限个间断点，则f(x)在[a，b]上可积。(B。)

A. 2

B. 3

C. 4

D. 5

解析：一元函数在闭区间上可导则一定连续，但在闭区间上连续不一定可导，所以(1)错误，(2)正确。“函数f(x)在[a，b]上可导”的充要条件是“函数f(x)在[a，b]上可微”，所以(3)正确。一元函数在开区间内连续，不一定可积，例如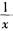在(0，1)内连续，但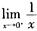=+∞，其在(0，1)内不可积，所以(4)错误。一元函数在闭区间上连续或在闭区间上有界且只有有限个间断点，则一定可积，但可积不一定连续，所以(5)正确。故本题选B。

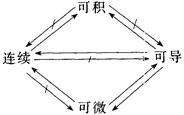
一元函数在闭区间上可积、可导、可微、连续的关系图如下：

6.实二次型f(x₁，x₂，x₃)=x₁²+2₂²一3x₃²+4x₁x₂+2x₂x₃是( )。(A。)

A. 不定二次型

B. 半正定二次型

C. 半负定二次型

D. 正定二次型

解析：根据二次型的性质，当对称矩阵的顺序主子式都大于0时，为正定二次型；顺序主子式大于等于0时，为半正定二次型；所有奇数阶顺序主子式小于0，所有偶数阶顺序主子式大于0时，为负定二次型；所有奇数阶顺序主子式小于或等于0，所有偶数阶顺序主子式大于或等于0时，为半负定二次型。本题中，二次型对应的对称矩阵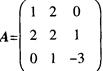，顺序主子式分别为1＞0，=一2＜0．

7.提出“集合论悖论”的数学家是( )。(B。)

A. 康托尔

B. 罗素

C. 庞加莱

D. 希尔伯特

解析：罗素构造了一个所有不属于自身(即不包含自身作为元素)的集合，提出了“集合论悖论”。

8.教学方法中的发现式教学法义叫( )教学法。(D。)

A. 习惯

B. 态度

C. 学习

D. 问题

解析：发现式教学法又叫问题教学法，是美国著名心理学家布鲁纳于20世纪50年代首先倡导的、让学生自己发现问题、主动获取知识的一种教学方法。故本题选D。本文档预览：3000字符，共9667字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载