中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷57

中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷57

单项选择题

1.设有10个零件，其中4个是次品，任取2个，至少有1个是正品的概率为( )。

(A。)

A.

B.

C.

D.

解析：取出的零件都为次品的概率为，则取出的零件中至少有1个是正品的概率为1—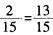

2.当x→0⁺时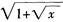，(D。)

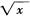A. B. x

C. x²

D. 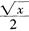解析：设当x→0⁺时，α(x)和β(x)都是无穷小量，若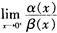=1，则α(x)和β(x)是当x→0⁺的等价无穷小量。根据洛必达法则，对各选项进行分析如下：

故本题选D。(其中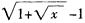，为x和x²当x→0⁺的低阶无穷小量，

3.设三阶方阵A的特征值为1，2，一3，则∣A²一3A—E∣的值为( )：(B。)

A. 135

B. 153

C. 一6

D. 0

解析：由矩阵特征值的性质可知，如果λ是矩阵λ的一个特征值，则λ²是A²的特征值，kλ是kA的特征值，λ－1是A－E的特征值。所以矩阵A²一3A－E的特征值为λ²一3λ一1(其中λ=1，2，一3)，即为一3，一3，17。因为矩阵的行列式等于矩阵所有特征值的乘积，所以|A²一3A一E=(一3)×(一3)×17=153。

4.方程y²=2－x，表示空间的曲面为( )。(D。)

A. 球面

B. 旋转双曲面

C. 圆锥面

D. 抛物柱面

解析：球面的标准方程为(x一a)²+(y一b)²+(z—c)²=r²。旋转双曲面的方程：单叶双曲面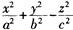=1．双叶双曲面=一1。圆锥面方程为

5.设A是m×n阶矩阵，非齐次线性方程组Ax=b有解的充分条件是( )。(A。)

A. r(A)=m

B. A的行向量组线性相关

C. r(A)=n

D. A的列向量组线性相关

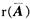解析：非齐次线性方程组Ax=b有解的充要条件是系数矩阵的秩等于增广矩阵的秩。由系数矩阵A是m×n阶矩阵知。增广矩阵=[A，b]是m×(n+1)阶矩阵，进而可知，r(A)≤≤m。若r(A)=m，则r(A)=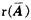=m，Ax=b有唯一解，但当r(A)=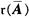＜m时，Ax=b有无穷解，所以r(A)=m是非齐次线性方程组Ax=b有解的充分条件。B，C，D三项均不能保证r(A)=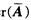

6.已知函数z=x²+3xy+2x+y，则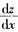(B。)

A. 2x+3y

B. 2x+3y+2

C. 3x+1

D. 2x+1

解析：根据二元函数偏导数的定义，求函数z(x，y)关于x的导数，将y看作常数，只对x求导即可．所以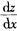

7.提出“一笔画定理”的数学家是( )。(C。)

A. 高斯

B. 牛顿

C. 欧拉

D. 莱布尼兹

解析：欧拉通过对七桥问题的研究提出了“一笔画定理”：一个图形要能一笔画完成必须符合两个条件，一是图形是连通的(图形的各部分连接在一起)，二是图形中的奇点(与奇数条边相连的点)个数为0或2。

8.初中阶段课程标准中“数与代数”包括数与式、方程与不等式和( )。(C。)

A. 三角形

B. 四边形

C. 函数

D. 图形与几何

解析：《义务教育数学课程标准(2011年版)》的内容标准中指出“数与代数”部分包括数与式、方程与不等式和函数。故本题选C。

简答题

9.求椭球面本文档预览：3000字符，共9295字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载