中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷53

中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷53

单项选择题

1.当x→0时，下列哪一个无穷小是x的三阶无穷小?( )(B。)

A. 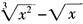B. 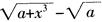C. x³+0．0001x²

D. 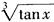解析：函数a(x)只要满足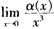=C≠0，即满足题意。经计算，只有B项中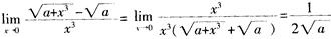

2.设4阶矩阵A与B仅有第3行不同，且∣A∣=1，∣B∣=2，则∣A+B∣=( )。(D。)

A. 3

B. 6

C. 12

D. 24

解析：根据题意，设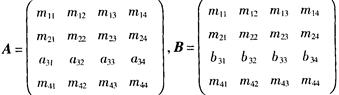．所以C=A+B=

3.对某目标进行100次独立射击，假设每次射击击中目标的概率是0．2，记X为100次独立射击中击中目标的总次数，则E(X²)等于( )。(D。)

A. 20

B. 200

C. 400

D. 416

解析：X服从二项分布，X～B(100，0．2)，所以E(X)=100×0．2=20，D(X)=100×0．2×0．8=16。所以

E(X²)=D(X)+[E(X)]²=16+20²=416。

4.已知三维向量空间的一组基为α₁=(1，1，0)，α₂=(1，0，1)，α₃=(0，1，1)，则向量β=(2，0，0)在此基底下的坐标是( )。(B。)

A. (2，0，0)

B. (1，1，－1)

C. (1，0，－1)

D. (0，0，0)

解析：设β=(2，0，0)在此基底下的坐标是(x₁，x₂，x₃)，则有β^T=x₁α₁^T+x₂α₂^T+x₃α₃^T=(α₁^T，α₂^T，α₃^T)，即得一非齐次的线性方程组，对增广矩阵做初等行变换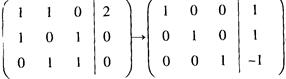

5.曲线x=t，y=t²,z=t³在点(1，1，1)处的法平面方程是( )。(B。)

A. 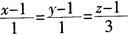B. x+2y+3z一6=0

C. D. x+y+z一3=0

解析：曲线x=t，y=t²,z=t³在点(1，1，1)处的向量为(1，2，3)，所以曲线在点(1，1，1)处的法平面方程为1·(x一1)+2·(y一1)+3·(z—1)=0，化简得x+2y+3z一6=0。

6.设函数f(x)在x=0处连续，且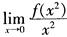(D。)

A. f(0)=1且f＇(0)=2

B. f(0)=0且f＇(0)=2

C. f(0)=1且f＇₊(x)=2

D. f(0)=0且f＇₊(0)=2

解析：根据题意首先得f(0)=0，由导数的定义，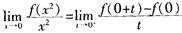

7.古希腊的三大著名几何尺规作图问题是( )。

①三等分角 ②立方倍积

③正十七边形 ④化圆为方(B。)

A. ①②③

B. ①②④

C. ①③④

D. ②③④

解析：在公元前6世纪至公元前4世纪之间，古希腊人遇到了令他们百思不得其解的三大尺规作图问题，这就是著名的古代儿何作图三大难题。(1)三等分角问题：将任一个给定的角三等分；(2)立方倍积问题：求作一个正方体的棱长，使这个正方体的体积是已知正方体体积的二倍；(3)化圆为方问题：求作一个正方形，使它的面积和已知圆的面积相等。

8.选取与所授内容有关的生活实例或某种经历，通过对其分析、引申、演绎归纳出从特殊到一般、从具体到抽象的规律来导入新课的方法是( )。(C。)

A. 直接导入法

B. 复习导入法

C. 实例导入法

D. 悬念导入法

解析：题干所描述的是实例导入法。

简答题

9.证明：若函数f(x)在[a，b]上可导，且f＇₊(a)≠f＇_－(b)，k为介于f＇₊(a)，f＇_－(b)之间的任意实数，则至少存在一点ξ∈(a，b)，使得f＇(ξ)=k。

假设F(x)=f(x)－kx，则F(x)在[a，b]上可导，且F＇₊(a)·F＇_–(b)

本文档预览：3000字符，共10243字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载