中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷56

中学教师资格认定考试（初级数学学科知识与教学能力）模拟试卷56

单项选择题

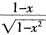1.函数y=与函数y=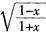(B。)

A. 定义域相同，值域相同

B. 定义域不同，值域不同

C. 定义域相同，值域不同

D. 定义域不同，值域相同

解析：函数y=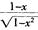的定义域为一1＜x＜1，且y不能等于0；函数y=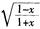

2.已知矩阵A=,矩阵B=(A。)

A. 既不相似也不合同

B. 合同但不相似

C. 相似但不合同

D. 合同且相似

解析：∣λE—A∣=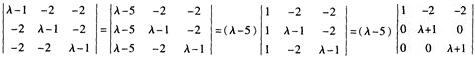

3.设随机变量X，Y不相关，且E(X)=2，E(Y)=1，D(X)=3，则E(X(X+Y－2))=( )。(D。)

A. －3

B. 3

C. －5

D. 5

解析：E(X(X+Y一2))=E(X²)+E(XY)一2E(X)=D(X)+(EX)²+E(X)E(Y)一2E(X)=5。

4.已知曲面方程为x²+y+2²一2x+8y+6z=10，则过点(5，一2，1)的切平面方程为( )。(B。)

A. 2x+y+2z=0

B. 2x+y+2z=10

C. x一2y+6z=15

D. x一2y+6z=0

解析：(方法一)设球面方程为x²+y²+z²+2px+2qy+2rz+d=0，则过球面上点(x₀，y₀，z₀)的切平面方程为

x₀x+y₀y+z₀z+p(x+x₀)+q(y+y₀)+r(z+z₀)+d=0。

由曲面方程为x²+y²+z²－2x+8y+6x=10可知p=－1，q=4，r=3，d=－10，则过点(5，－2，1)(点在球面上)的切平面为

5x－2y+z－(x+5)+4(y－2)+3(z+1)－10=0

整理得：2x+y+2z=10。故本题选B。

(方法二)曲面x²+y²+z²－2x+8y+6z=10为球面，标准方程为

(x－1)²+(y+4)²+(z+3)²=36

球心为(1，－4，－3)，半径为6。由A，B，C，D四个选项中，只有选项B，C过点(5，－2，1)。故A，D排除。同时球心到切平面的距离应该等于球的半径，选项B，球心到平面的距离为

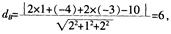
5.设f(x)=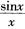(D。)

A. 连续点

B. 跳跃间断点

C. 第二类间断点

D. 可去间断点

解析：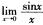

6.已知线性方程组AX=Kβ₁+β₂有解，其中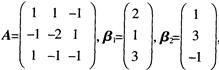(D。)

A. 1

B. －1

C. 2

D. －2

解析：已知线性方程组是非齐次的，要使方程有解，则系数矩阵的秩要等于增广矩阵的秩．由此可以求出K。

因为线性方程组AX=Kβ₁+β₂，将AX=Kβ₁+β₂。的增广矩阵作初等行变换，

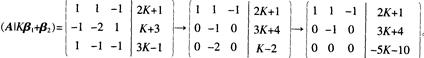
AX=Kβ₁+β₂有解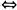

7.刘徽在注释《九章算术》的过程中，提出了许多创造性的见解，值得一提的是，他创造性地发展了极限思想并加以灵活运用，其例子是( )。(A。)

A. 割圆术

B. 解体用图

C. 盈不足术

D. 齐同变换

解析：“割圆术”是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法。是对极限思想的灵活运用。

8.下列划分正确的是( )。(D。)

A. 有理数包括整数、分数和零

B. 角分为直角、象限角、对顶角和同位角

C. 数列分为等比数列、等差数列、无限数列和递减数列

D. 平行四边形分为对角线互相垂直的平行四边形和对角线不互相垂直的平行四边形

解析：分类的各个子项应相互排斥，故可排除A，C两项，分类应按照统一标准进行。则可排除B项。

简答题

9.求通过直线本文档预览：3000字符，共9562字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载