中学教师资格认定考试(初级数学学科知识与教学能力)模拟试卷49
单项选择题
1.极限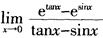 (C。)
(C。)
A. 0
B. 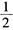 C. 1
C. 1
D. 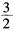 解析:利用等价无穷小量,当x→0时,x~ex-1。本题中
解析:利用等价无穷小量,当x→0时,x~ex-1。本题中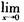 (tanx—sinx)=0,所以
(tanx—sinx)=0,所以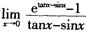 =1。
=1。
所以极限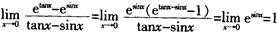
2.直线l: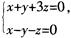 与平面x一y+2z+1=0的夹角θ是( )。
与平面x一y+2z+1=0的夹角θ是( )。
 (A。)
(A。)
A.
B.
C.
D.
解析:直线l的方向向量m=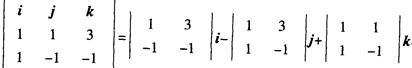 =(2,4,一2),平面的法向量n=(1,一1,2),则sinθ=∣cos<m,n>∣=
=(2,4,一2),平面的法向量n=(1,一1,2),则sinθ=∣cos<m,n>∣= .所以θ=
.所以θ=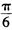
3.设λ1,λ2是矩阵A的两个不同的特征值,α,β分别为A对应于λ1,λ2的特征向量,则α,β( )。(B。)
A. 线性相关
B. 线性无关
C. 正交
D. 平行
解析:属于不同特征值的特征向量线性无关。
4.设矩阵 (D。)
(D。)
A. a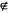 Ω,d
Ω,d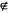 B. a
B. a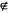 C. a∈Ω,d
C. a∈Ω,d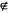 D. a∈Ω,d∈Ω
D. a∈Ω,d∈Ω
解析:线性方程组Ax=b有无穷多解的充分必要条件:r(A)=r(A,b)<3。
(A,b)=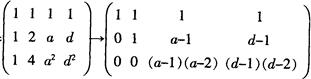
5.事件A,B相互独立,且P(A∪B)=0.8,P(A)=0.4,则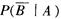 等于( )。
等于( )。
 (B。)
(B。)
A.
B.
C.
D.
解析:事件A、B相互独立,则P(A∪B)=P(A)+P(B)一P(AB)=P(A)+P(B)一P(A)P(B),所以
P(B)=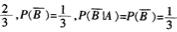
6.设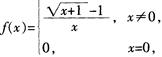 (A。)
(A。)
A. 可去间断点
B. 无穷间断点
C. 连续点
D. 跳跃间断点
解析:因为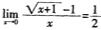
7.费马对微积分诞生的贡献主要在于其发明的( )。(C。)
A. 求瞬时速度的方法
B. 求切线的方法
C. 求极值的方法
D. 求体积的方法
解析:费马是微积分的先驱者,他在求曲线围成的图形的面积过程中,提出用微分子法求极大、极小值的步骤,这是早期微积分的雏形。
8.在等腰三角形、平行四边形、椭圆和抛物线四个图形中,是中心对称图形的有( )。(B。)
A. 1个
B. 2个
C. 3个
D. 4个
解析:四个图形中,椭圆既是轴对称图形又是中心对称图形,平行四边形是中心对称图形,等腰三角形和抛物线是轴对称图形,所以这四个图形中有2个是中心对称图形。
简答题
9.已知f(x)=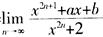
首先,根据已知求出f(x)的表达式,分类讨论如下:
当x=1时,f(x)=[*];
当|x|<1时,f(x)=[*];
当|x|>1时,f(x)=[*]=x:
当x=一1时,f(x)=[*];
于是,[*] 因为f(x)是连续函数,所以进一步讨论如下:
在x=1处,[*],要使f(x)在x=1处连续.则
[*]解得a+b=2:
在x=-1处[*],要使f(x)在x=一1处连续.
则[*] 解得a-b=2。
联立[*]解得[*]
故当a=2,b=0时,f(x)是连续函数。
解析:
10.曲面z=