全国自考公共课线性代数（经管类）模拟试卷21

全国自考公共课线性代数（经管类）模拟试卷21

单选题

1.行列式(D)

A. 0

B. 21

C. 42

D. 一42

解析：行列式展开性质，

=(一1)¹⁺⁴×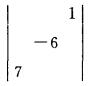

2.设A、B为n阶方阵，且AB=O(零矩阵)，则 ( )(D)

A. A=P或B=O

B. A+B=O

C. ｜A｜+｜B｜=0

D. ｜A｜=0或｜B｜=0

解析：由于｜AB｜=｜A｜．｜B｜=｜0｜=0，所以｜A｜=0或｜B｜=0．答案为D。

3.α₁=(1，2，3)，α₂=(2，1，3)，α₃=(一1，1，0)，α₄=(1，1，1)，

则 ( )(C)

A. α₁线性相关

B. α₁，α₂线性相关

C. α₁，α₂，α₃线性相关

D. α₁，α₂，α₄线性相关

解析：单个非零向量是线性无关的，∴选项A不对，而(α₁，α₂，α₃)→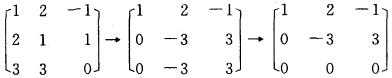

4.方程组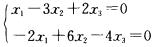(B)

A. 1

B. 2

C. 3

D. 4

解析：该方程组的系数矩阵秩等于1，有3个未知数，因此基础解系由2个线性无关的向量组成．答案为B。

5.实二次型f(x₁，…，x_n)=x^TAx为正定的充要条件是 ( )(B)

A. f的秩为n

B. f的正惯性指数为n

C. f的正惯性指数等于f的秩

D. f的负惯性指数为n

解析：由正定的性质即得．答案为B。

填空题

6.已知四阶行列式D的第一行元素依次为1，3，0，一2，第三行元素对应的代数余子式依次为8，k，一7，10，则k=_________．

4

解析：根据代数余子性质8+3k一20=0→k=4．

7.设A=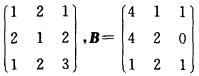

[*]

解析：(A+B)²一(A²+AB+B²)

=(A+B)(A+B)一(A²+AB+B²)

=A²+B²+AB+BA—A²一AB—B²

=BA

8.设A=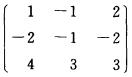

[*]

解析：由于A^-1=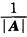A^*，所以A^*=｜A｜．A^-1，(A^*)^-1=(｜A｜．A^-1)^-1=

9.已知α=(2，1，3)，β=(一1，3，6)则2α+3β=_________．

(1，11，24)

解析：2α+3β=(4，2，6)+(一3，9，18)=(1，11，24)．

10.当k为_________时，向量组α₁=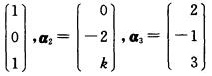

2

解析：∵α₁，α₂，α₃不能构成R³的一组基

∴α₁，α₂，α₃线性相关

∴

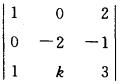
11.已知线性方程组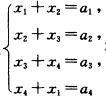

一a₁+a₂—a₃+a₄=0

解析：对线性方程组的增广矩阵作初等行变换，有

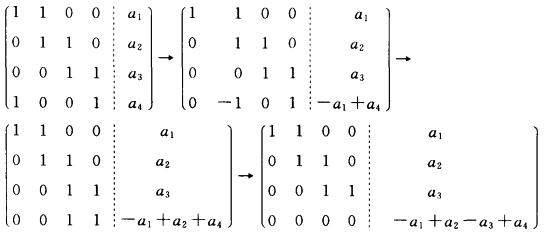
12.已知三阶矩阵A的特征值分别为1、一1、2，则｜A一5E｜ =_________．

一72

解析：A的特征值分别为1、一1、2，则A一5E的特征值分别为一4，一6，一3．故｜A一5E｜=一72．

13.设n阶方阵A与B相似且A²=A，则B²=_________．

B

解析：由于A与B相似，存在可逆矩阵P，使得B=P^-1AP，所以B²=P^-1AP．P^-1AP=P^-1A²P=P<

本文档预览：3500字符，共6615字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载