全国自考公共课线性代数（经管类）模拟试卷29

全国自考公共课线性代数（经管类）模拟试卷29

单选题

1.设A为3阶方阵且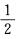｜A｜=(A)

A. 一4

B. 4

C. 一1

D. 1

解析：｜一2A｜=(一2)³｜A｜=一8×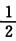

2.若AB=AC，能推出B=C，其中A，B，C为同阶方阵，则A应满足条件 ( )(D)

A. A≠0

B. A=0

C. ｜A｜=0

D. ｜A｜≠0

解析：若AB=AC，则A(B—C)=0，故当A可逆，即｜A｜≠0时B=C．答案为D。

3.设矩阵A_m×n的秩为r(A)=m＜n，I_m为m阶单位矩阵，下述结论中正确的是 ( )(D)

A. A的任意m个列向量必线性无关

B. A的任意一个m阶子式不等于零

C. 若矩阵B满足BA=O，则B=O

D. A通过初等行变换，必可以化为(I_mO)的形式

解析：矩阵A_m×n的秩r(A)=m＜n．故A的行满秩，列不满秩，A的m个列向量可能线性无关也可能线性相关，且A通过初等行变换，可以化为(I_mO)形式，故选D．答案为D。

4.若α₁，α₂，α₃是齐次方程组Ax=0的基础解系，则下列答案中也是Ax=0的基础解系的为 ( )(C)

A. α₁一α₂，α₂一α₃，α₃—α₁

B. α₁，α₂，α₃的任意三个线性组合

C. α₁，α₁一α₂，α₁—α₂—α₃

D. α₁，2α₁，3α₁

解析：本题考查基础解系的定义，基础解系必须线性无关，且与α₁，α₂，α₃等价．答案为C。

5.设A=(B)

A. (1，1，2)^T

B. (1，2，3)^T

C. (1，0，1)^T

D. (1，1，1)^T

解析：用定义Ax=λx来判断，这时λ=0，故计算Ax的值，使Ax=0的向量x就是A的属于特征值0的特征向量．当x=(1，2，3)^T时，有Ax=0．答案为B。

填空题

6.行列式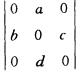

0

解析：按定义计算，可得结果为0．

7.设A为n阶方阵，且｜A｜=2，则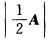

[*]

解析：

8.设矩阵A=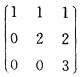

[*]

解析：A^T．A=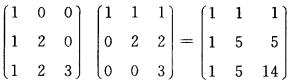

9.分块矩阵A=

A^T=[*]

解析：由转置矩阵的定义知．

10.已知α₁，α₂线性无关而α₁，α₂，α₃线性相关，则向量组α₁，3α₂，7α₃的极大无关组为__________．

α₁，3α₂

解析：由于α₁与3α₂线性无关，并且7α₃可由α₁，3α₂线性表示．

11.设矩阵A为4×6矩阵，如果秩A=3，则齐次线性方程组AX=0的基础解系含有解向量的个数为__________．

3

解析：由于AX=0是6个未知量的齐次线性方程组．6一r(A)=6—3=3，所以基础解系中含有3个解向量．

12.设λ=2是n阶方阵A的一个特征且｜A｜≠0，则n阶方阵B=A³一3E+A^-1必有特征值__________．

[*]

解析：｜A｜≠0，因此A可逆，又λ=2是A的特征值，因此存在非零向量α使得Aα=2α，所以A²α=A²(Aα)=α²(2α)=2A(Aα)=4Aα=8α，A^-1α=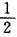α，所以Bα=A³α一3Eα+A^-1α=8α一3α+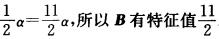

13.设3阶方阵A的特征值为λ₁=1，λ₂=1，λ₃=2，则｜A｜=__________．

一2

解析：｜A｜=λ₁．λ₂．λ₃=一2．

14.已知三阶矩阵A=本文档预览：3500字符，共5908字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载