全国自考公共课线性代数（经管类）模拟试卷25

全国自考公共课线性代数（经管类）模拟试卷25

单选题

1.设A是m×n阶矩阵，B是n×m阶矩阵(m≠n)，则下列运算结果是n阶方阵的是 ( )(B)

A. A．B

B. A^T．B^T

C. B^T．A^T

D. (A+B)^T

解析：由矩阵乘法的运算定义和矩阵转置的定义可知A^T．B^T是n阶方阵．答案为B。

2.设A是3阶反对称矩阵，即A^T=一A，则｜A｜= ( )(A)

A. 0

B. 1

C. ±1

D. 0或l

解析：由于｜A｜=｜A^T｜=｜—A｜=(一1)³｜A｜=一｜A｜，所以｜A｜=0．答案为A。

3.设A是n阶矩阵，A^*是A的伴随矩阵，则 ( )(C)

A. AA^*=｜A｜

B. AA^*｜A｜ⁿ

C. A^*A=｜A｜I

D. A^*A=｜A｜ⁿI

解析：A．A^*=｜A｜I．答案为C。

4.若齐次线性方程组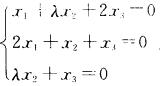(B)

A. λ=一1

B. λ≠一1

C. λ=1

D. λ≠1

解析：齐次线性方程组Ax=0只有零解→｜A｜≠0

｜A｜=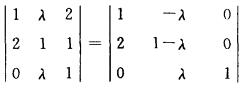

5.二次型f=x^*Ax经过满秩线性变换x=Py可化为二次型y^*By，则矩阵A与B ( )(A)

A. 一定合同

B. 一定相似

C. 即相似又合同

D. 即不相似也不合同

解析：f=x^TAx=(Py)^TA(Py)=y^T(P^TAP)y=y^TBy，即B=P^TAP，所以矩阵A与B一定合同．只有当P是正交矩阵时，由于P^T=P^-1，所以A与B既相似义合同．答案为A。

填空题

6.已知齐次线性方程组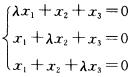

λ=1或λ=一2

解析：由于齐次线性方程度组有非零解．因此系数行列式

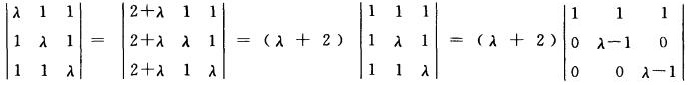
7.设矩阵A=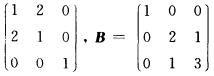

[*]

解析：A+2B=

8.设A=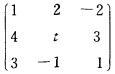

一3

解析：AB=0，故r(A)+r(B)≤3

又∵zb为三阶非零矩阵，故r(B)≥1所以r(A)＜3，｜A｜=0

｜A｜=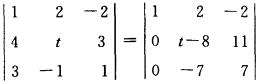

9.设向量α₁=(1，1，1)^T，α₂=(1，1，0)^T，α₃=(1，0，0)^T，β=(0，1，1)^T，则β由α₁，α₂，α₃线性表示的表示式为_________．

β=α₁+0α₂—α₃

解析：设线性方程组为x₁α₁+x₂α₂+x₃α₃=β，对它的增广矩阵施行初等变换，得：

(A，α)=(α₁，α₂，α₃，β)=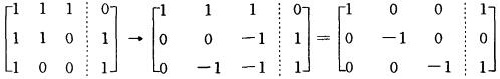=(T，d)．

显然x₁α₁+x₂α₂+x₃α₃=β的同解方程组Tx=d就是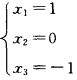

10.方程组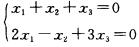

1

解析：由于系数矩阵的秩为2，所以有3—2=1个自由未知量．

11.阶矩阵A的特征值为一1，1，2，则B=E+A^*的特征值为_________．

3，一1，0

解析：设λ为三阶矩阵A的特征值，｜A｜=一1×1×2=一2．A^-1的特征值为一1，1，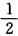

12.设3阶方阵的特征值为1，一1，2，则｜A一5E｜=_________．

一72

解析：如果λ₀是A的特征值，则存在非零向量α使Aα=λ₀α，因此(A一5E)α=Aα—5α=(λ₀一5)α，所以λ₀一5是A一5E的特征值，由此可知A一5E的三个特征值为1—5=一4，一1—5=一6，2—5=一3，所以｜A一5E｜=(一4)×(一6)×(一3)=一72．

13.已知4阶方阵A相似于B，A的特征值为2，3，4，5，则｜B—E｜=_________．

本文档预览：3500字符，共6721字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载