全国自考公共课线性代数（经管类）模拟试卷23

全国自考公共课线性代数（经管类）模拟试卷23

单选题

1.若A，B均为n阶方阵，且AB=0，则 ( )(C)

A. A=O或B=O

B. A+B=O

C. ｜A｜=0或｜B｜=0

D. ｜A｜+｜B｜=0

解析：AB=0→｜AB｜=0→｜A｜．｜B｜=0→｜A｜=0或｜B｜=0．答案为C。

2.若n阶方阵A可逆，且伴随矩阵A^*也可逆，则A^*的逆矩阵为 ( )(C)

A. A

B. ｜A｜．2

C. 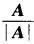D. 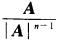解析：由于A可逆，因此｜A｜≠0，又A．A^*=A^*．A=｜A｜．I，所以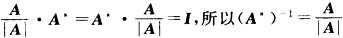

3.设α₁=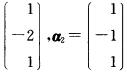(D)

A. (2，1，2)^T

B. (1，0，1)^T

C. (0，1，0)^T

D. (0，0，1)^T

解析：首先已知α₁，α₂线性无关(其坐标不成比例)，又令A=(α₁，α₂，α₃)，则α₁，α₂，α₃线性无关→｜A｜≠0

由于A的左上角2阶主子式(记为｜A₁₁｜)不等于0，故选α₃=即可。

(此时｜A｜^*=

4.设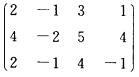A=(A)

A. 1

B. 2

C. 3

D. 0

解析：由于V(A)=3，所以基础解集含有4—3=1个向量．答案为A。

5.设A=(C)

A. f(x₁，x₂，x₃)=x₁²+x₂²+x₃²

B. f(x₁，x₂，x₃)=x₁²+x₂x₃

C. f(x₁，x₂，x₃)=x₂²+x₁x₃

D. f(x₁，x₂，x₃)=x₃²+x₁+x₂

解析：A的主对角线元素1对应x₂系数；a₁₃=1，a₃₁=1，之和对应x₁x₃系数2．答案为C。

填空题

6.已知矩阵A=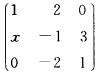

7

解析：由于A₁₂=(一1)¹⁺²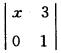=一x=1，因此x=一1．

所以｜A｜=

7.设矩阵A=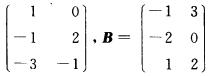

[*]

解析：3A^T—B^T=3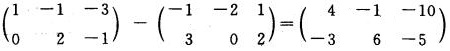

8.设D=

3

解析：a为行列式D的a₂₃项，故a的代数余子式为A₂₃，且A₂₃=(—1)²⁺³

9.k=________时，向量组α₁=(6，k+1，7)，α₂=(k，2，2)，α₃=(k，1，0)线性相关．

k=4或k=一[*]．

解析：

10.已知α₁=

[*]

解析：以α₁，α₂，α₃，β为列向量的矩阵作初等行变换，有

本文档预览：3500字符，共7740字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载