
全国自考概率论与数理统计(经管类)模拟试卷14
单选题
1.A、B为随机事件,则(A∪B)∩(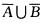 (C)
(C)
A. 必然事件
B. 不可能事件
C. A与B恰有一个发生
D. A与B不同时发生
解析:A、B为随机事件,A∪B表示A发生或B发生,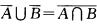 表示A,B不能同时发生,故A∪B∩
表示A,B不能同时发生,故A∪B∩
2.若A,B为两事件,A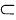 (C)
(C)
A. P(A∪B)=P(A)+P(B)
B. P(AB)=P(A).P(B)
C. P(B|A)=1
D. P(A-B)=P(A)-P(B)
解析:P(A∪B)=P(A)+P(B)-P(AB)=P(B)(选项A不对);B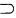 A=>AB=A=>P(AB)=P(A)(选项B不对);P(A-B)=P(A
A=>AB=A=>P(AB)=P(A)(选项B不对);P(A-B)=P(A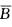 )=0 (选项D不对);P(B|A)=
)=0 (选项D不对);P(B|A)=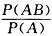
3.某种商品进行有奖销售,每购买一件有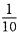 (D)
(D)
A. 正态分布
B. 指数分布
C. 泊松分布
D. 二项分布
解析:根据二项分布定义知D正确.
4.设随机变量ξ~N(2,σ2),且P{2<ξ<4}=0.3,则P{ξ<0}= ( )(B)
A. 0.1
B. 0.2
C. 0.3
D. 0.5
解析:本题考查概率的求解方法.
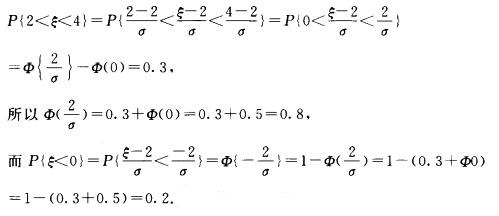
5.设二维随机变量(X,Y)的概率密度为f(x,y),则P{X>1}= ( )(B)
A. ∫-∞1dx∫-∞+∞f(x,y)dy
B. ∫1+∞dx∫-∞+∞f(x,y)dy
C. ∫-∞1f(x,y)dy
D. ∫1+∞f(x,y)dx
解析:P(X>1)=∫1+∞dx∫-∞+∞f(x,y)dy.
6.设随机变量X服从参数为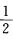 (C)
(C)
A. 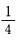 B.
B. 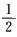 C. 2
C. 2
D. 4
解析:结合指数分布的一般形式,得λ=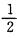 ,∴E(x)=
,∴E(x)=
7.设随机变量X的均值E(X)=μ,方差D(X)=σ2,则E(X2)= ( )(B)
A. σ2-μ2
B. σ2+μ2
C. σ-μ
D. σ+μ
解析:E(X)=μ,D(X)=σ2,
又∵D(X)=E(X2)-E2(X),
E(X2)=D(X)+E2(X)=σ2+μ2.
8.设随机变量X的方差D(X)=2,则利用切比雪夫不等式估计概率P{|X-E(X)|≥8}的值为 ( )
B
解析:P{|X-E(x)|≥8}≤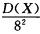 即{|X-E(X)|≥8)≤
即{|X-E(X)|≥8)≤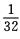
9.设总体X服从参数p=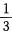 的0—1分布,即
的0—1分布,即
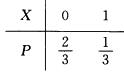 X1,X2,…,Xn为X的样本,记
X1,X2,…,Xn为X的样本,记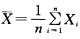 为样本均值,则
为样本均值,则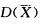 = ( )
= ( )
 (C)
(C)
本文档预览:3500字符,共11618字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载