全国自考概率论与数理统计（经管类）模拟试卷12
单选题
1.设随机事件A与B互不相容，且P(A)＞0，P(B)＞0，则 ( )(A)
A. P(B｜A)=0
B. P(A｜B)＞0
C. P(A｜B)=P
D. P(AB)=P(A)P(B)
解析：P(B｜A)=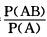
2.设A，B为两个随机事件，且P(AB)＞0，则P(A｜AB)= ( )(D)
A. P(A)
B. P(AB)
C. P(A｜B)
D. 1
解析：P(A｜AB)表示的意义是在A、B两个事件同时发生的条件下事件A发生的概率，易知P(A｜AB)=1．
3.设随机变化量X的概率密度为
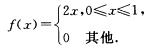则P{0≤X≤
}= ( )
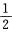(A)
A.
B.
C.
D.
解析：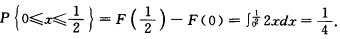
4.设随机变量X服从参数为3的指数分布，其分布函数记为F(x)，则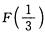
= ( )
(C)
A.
B.
C.
D.
解析：∵X服从参数为3的指数分布，
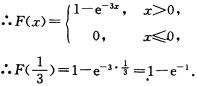
5.设下列函数的定义域均为(－∞，+∞)，则其中可以作为概率密度的是 ( )(C)
A. f(x)=－e－x
B. f(x)=e－x
C. f(x)=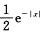
D. f(x)=e－｜x｜
解析：由概论密度的性质得，f(x)≥0，∫－∞+∞f(x)dx=1，A项，f(x)=－e－x＜0排除，B项，∫－∞+∞e－xdx=－e－x｜+∞－∞=+∞，C项f(x)=
6.设随机变量X～B(10，
(D)
A. －0．8
B. －0．16
C. 0．16
D. 0．8
解析：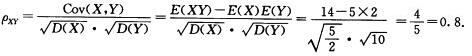
7.已知随机变量X的概率密度为f(x)=
(B)
A. 6
B. 3
C. 1
D.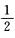 
解析：因为E(x)=∫－∞+∞xf(x)dx，所以就有
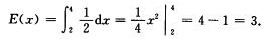
8.设随机变量X～N(0，1)，Y～N(0，1)，且X与Y相互独立，则X2+Y2～ ( )(B)
A. N(0，2)
B. χ2(2)
C. t(2)
D. F(1，1)
解析：由χ2分布定义知，X2+Y2～χ2(2)．
9.设随机变量Zn～B(n，p)，n=1，2，…，其中0＜p＜1，则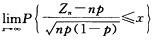
= ( )
(B)
A.
B.
C.
D.
解析：由独立同分布的中心极限定理知
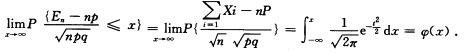
10.设总体X～N(μ，σ2)，其中σ2未知．现随机抽样，计算得样本方差为100，若要对其均值进行检验，采用 ( )(D)
A. Z—检验法
B. χ2—检验法
C. F—检验法
D. t—检验法
解析：Z—检验法适用对象：单个或多个正态总体，σ2已知时，关于均值μ的假设检验．t—检验法适用对象：单个或多个正态总体，σ2未知，用样本值S2代替时，关于均值μ的假设检验．χ2—检验法：用来检验在未知正态总体的均值时，其方差是否等于某个特定值．F一检验法，用来检验均值未知的两个正态总体，其方差是否相等．
填空题
11.设A与B是两个随机事件，已知
本文档预览：3500字符，共9603字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
