全国自考概率论与数理统计（经管类）模拟试卷17

全国自考概率论与数理统计（经管类）模拟试卷17

单选题

1.掷两颗骰子，它们出现的点数之和等于7的概率为 ( )

(A)

A.

B.

C.

D.

解析：由题意知：P=P(ξ₁=1，ξ₂=6)+P(ξ₁=2，ξ₂=5)+P(ξ₁=3，

ξ₂=4)+P(ξ₁=6，ξ₂=1)+P(ξ₁=5，ξ₂=2)}P(ξ₁=4，ξ₂=3)=

2.若P(A)=P(B)=P(C)=0．4，且A，B，C相互独立，则P(A∪B∪C)= ( )(D)

A. 0．064

B. 0．216

C. 0．936

D. 0．784

解析：P(A∪B∪C)=P(A)+P(B)+P(C)－P(AB)－P(AC)－P(BC)+P(ABC)=P(A)+P(B)+P(C)－P(A).P(B)－P(A).P(C)－P(B).P(C)+P(A).P(B).P(C)=0．784．

3.随机变量ξ的分布函数F(x)=P{ξ≤x}的概率意义是 ( )(B)

A. ξ取值落入(－∞，+∞)的概率

B. ξ取值落入(－∞，x]的概率

C. ξ取值落入(－∞，x)的概率

D. ξ取值落入[－x，x]的概率

解析：本题考查随机变量分布函数的定义．

4.随机变量X服从正态分布N(0，4)，则P{X＜1}=( )

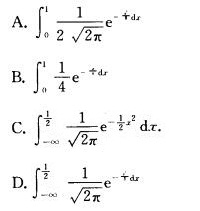(C)

A.

B.

C.

D.

解析：根据正态分布的分布函数定义式：

5.设二维随机变量(X，Y)的分布函数为F(x，y)，其边缘分布函数为F_X(x)、F_Y(y)，且对某一组x₁、y₁有F(x₁，y₁)=F_X(x₁).F_Y(y₁)，则下列结论正确的是 ( )(A)

A. X和Y相互独立

B. X和Y不独立

C. X和Y可能独立，也可能不独立

D. X和Y在点(x₁，y₁)处独立

解析：由随机变量x，y相互独立的定义知，对任意实数x，y有F(x，y)=F_X(x)F_Y(y)．称X与Y相互独立．

6.随机变量ξ～N(μ₁，σ₁²)，η～N(μ₂，σ₂²)，且ξ与η相互独立，则ξ+η～ ( )(C)

A. N(μ₁，σ₁²+σ₂²)

B. N(μ₂，σ₁²+σ₂²)

C. N(μ₁+μ₂，σ₁²+σ₂²)

D. N(μ₁+μ₂，σ₂²)

解析：D(ξ)=σ₁²，D(η)=σ₂²，由期望的性质可知D(ξ+η)=D(ξ)+D(η)=σ₁²+σ₂²，E(ξ+η)=μ₁+μ₂．

7.若E(X)、E(Y)都存在，则下面命题中错误的是 ( )(D)

A. E(X+Y)=E(X)+E(Y)

B. E(X－Y)=E(X)－E(Y)

C. E(6X)=6E(X)

D. E(XY)=E(X)E(Y)

解析：当X与Y是相互独立时，E(XY)=E(X)E(Y)，此题未讲相互独立条件故D选项错．

8.设随机变量X₁，X₂，…，X_n，…相互独立，它们满足大数定理，则X_i的分布可以是 ( )

A

解析：只要判断此序列是否独立同分布，且数学期望存在；或独立但分布不同，而数学期望、方差都存在，且方差一致有界即可．

选项A中X_i独立同分布，且E(X_i)=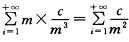，级数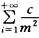收敛，因此E(X_i)存在．

选项D中X_i独立同分布，但E(X_i)不存在，因为

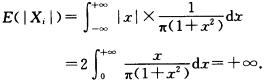
9.设总体X～N(μ，σ²)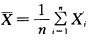，为样本均值，S_n²=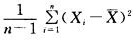为样本方差，样本容量为n，则以下各式服从标准正态分布的是 ( )

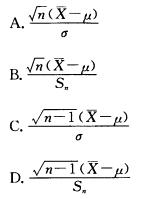(A)

A

本文档预览：3500字符，共10194字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载