
全国自考概率论与数理统计(经管类)模拟试卷11
单选题
1.设事件A、B同时发生必然导致事件C发生,则 ( )(A)
A. P(C)≥P(AB)
B. P(C)=P(AB)
C. P(C)=P(A+B)
D. P(C)≤P(AB)
解析: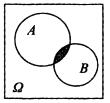
2.事件A与B互斥,P(A)=0.4,P(B)=0.3,则P(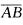 (A)
(A)
A. 0.3
B. 0.12
C. 0.42
D. 0.7
解析: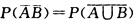
3.对于随机变量X,函数F(x)=P{X≤x}称为X的 ( )(D)
A. 概率分布
B. 概率
C. 概率密度
D. 分布函数
解析:本题考查分布函数的定义.
4.X为连续型随机变量,f(x)为其概率密度,则 ( )(D)
A. f(x)=F(x)
B. f(x)≤1
C. P{X=x}=f(x)
D. f(x)≥0
解析:本题考查概率密度的性质(1)f(x)≥0.
5.下列函数中,可以作为某个二维连续型随机变量的密度函数的是 ( )(B)
A. f1(x,y)=sinx, (x,y)∈R2
B. f2(x,y)=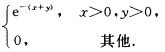 C. f3(x,y)=
C. f3(x,y)=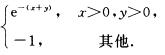 D. f4(x,y)=
D. f4(x,y)=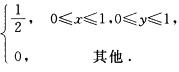 解析:概率密度f(x,y)应满足以下性质
解析:概率密度f(x,y)应满足以下性质
(1)f(x,y)≥0;
(2)∫-∞+∞∫-∞+∞f(x,y)dxdy=1.
6.设X为随机变量,且E(X)存在,则E(X)是 ( )(B)
A. X的函数
B. 确定常数
C. 随机变量
D. x的函数
解析:期望E(X)是随机变量x的数字特征,是常数.对于离散型X,E(X)=∑xp;对于连续型X,如果它的密度函数为p(x),则E(X)=∫-∞+∞xp(x)dx,这些结果都不含变量,而是确定常数.
7.随机变量X的方差D(X)存在,C为非零常数,则一定有 ( )(D)
A. D(X+C)=D(X)+C
B. D(X-C)=D(X)-C
C. D(CX)=CD(X)
D. D(CX+1)=C2D(X)
解析:随机变量X的方差D(X)存在,C为非零常数,根据方差的性质:
D(X±C)=D(X),
D((CX)=C2D(X),
D(CX+1)=C2D(X)。
8.X服从参数为1的泊松分布,则有 ( )
C
解析:由切比雪夫大数定律的定理5—3得
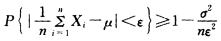
9.设总体X~N(μ,σ2),X1,X2,…,Xn是来自X的简单随机样本, (C)
(C)
A. E(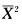 B. E(
B. E(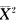 C. E(
C. E(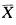 D. E(
D. E(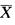 解析:为总体X~N(μ,σ2),所以
解析:为总体X~N(μ,σ2),所以
E(X)=E(X)=μ, E(S2)=D(X)=σ2,
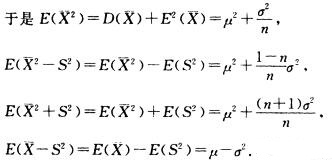
10.设总体X为参数为λ的动态分布,今测得X的样本观测值为0.1,0.2,0.3,0.4,则参数λ的矩估计值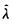 (B)
(B)
A. 0.2
B. 0.25
C. 1
D. 4
解析:虽然不知道动态分布的具体密度函数,但其只有一个未知参数λ,所以,也就只需要一个方程就可以确定.用一阶样本矩来估计一阶总体矩
填空题
11.设随机事件A与B相互独立,且P(A)=P(B)= ,则P(A∪
,则P(A∪
[*]
解析: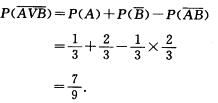
12.甲、乙两门高射炮彼
本文档预览:3500字符,共8614字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载