
全国自考概率论与数理统计(经管类)模拟试卷16
单选题
1.设A,B,C是三个事件,A,B,C中至少有两个发生的事件是 ( )(C)
A.  B. ABC
B. ABC
C. AB+AC+BC
D. 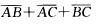 解析:根据事件A、B、C的运算表示进行排除.
解析:根据事件A、B、C的运算表示进行排除.
2.设事件A,B相互独立,且P(A)=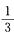 ,P(B)>0,则P(A|B) = ( )
,P(B)>0,则P(A|B) = ( )
 (D)
(D)
A.
B.
C.
D.
解析:事件A、B相互独立,则P(AB)=P(A)P(B),又因为P(B)>0,
故条件概率P(A/B)=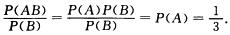
3.设随机变量X服从参数λ=2的泊松分布,F(x)为X的分布函数,则下列正确的是 ( )(B)
A. F(1)=e-2
B. F(0)=e-2
C. P(X=0)=P(X=1)
D. P(X≤1)=2e-2
解析:根据泊松分布定义Pk=P(X=k)=
4.X服从正态分布N(μ,σ2),其概率密度f(x)= ( )
 (D)
(D)
A.
B.
C.
D.
解析:本题考查正态分布概率密度定义.
5.设二维随机变量(X,Y)的概率密度为
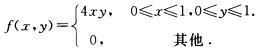 (D)
(D)
A. 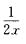 B. 2x
B. 2x
C. 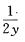 D. 2y
D. 2y
解析:0≤y≤1时,fY(y)=∫-∞+∞f(x,y)dx=∫014xydx=2y.x2|01=2y.
6.随机变量X与Y相互独立且同分布于N(μ,σ2),σ2>0,则下面结论不成立的是 ( )(C)
A. E(2X-2Y)=0
B. E(2X+2Y)=4μ
C. D(2X-2Y)=0
D. X与Y不相关
解析:X与Y相互独立,且X~N(μ,σ2),Y~N(μ,σ2),则:
EX=EY=μ,
DX=DY=σ2,
那么由期望、方差的性质可得:E(2X-2Y)=2E(X)-2E(Y)=0;
E(2X+2Y)=2E(X)+2E(Y)=4μ,
X与Y相互独立,则D(X+Y)=D(X)+D(Y),
E(XY)=E(X)E(Y),
Cov(X,Y)=E(XY)-E(X)E(Y)=0,
D(2X-2Y)=4D(X)+4D(Y)=8σ2,
则ρXY=0,X与Y不相关.
7.设随机变量X~N(2,4),则D(2X+5)= ( )(C)
A. 4
B. 18
C. 16
D. 13
解析:D(2X+5)=4D(X),
又∵D(X)=4,
故D(2X+5)=4×4=16.
8.若随机变量X的方差D(X)存在,则P{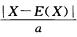 (C)
(C)
A. D(X)
B. 1
C.  D. a2D(X)
D. a2D(X)
解析:P{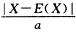 >1}=P{|X-E(X)|>a},根据切比雪夫不等式,P{|X-E(X)|>ε}≤
>1}=P{|X-E(X)|>a},根据切比雪夫不等式,P{|X-E(X)|>ε}≤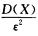 ,所以{|X-E(X)|>a}≤
,所以{|X-E(X)|>a}≤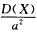
9.设x1,x2,…,x100为来自总体X~N(0,42)的一个样本,以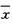 表示样本均值,则
表示样本均值,则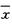 (B)
(B)
A. N(0,16)
B. N(0,0.16)
C. N(0,0.04)
D. N(0,1.6)
解析: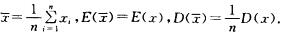
∵X~N(0,42本文档预览:3500字符,共12167字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载