管理类专业学位联考综合能力（数学）模拟试卷131
管理类专业学位联考（综合能力）-问题求解
1.甲、乙两辆汽车早上8点钟分别从A，B两城同时相向而行．到10点钟时两车相距120千米．继续行进到下午1点钟，两车相距还是120千米．A，B两地间的距离是( )千米．(E)
A. 150
B. 180
C. 200
D. 240
E. 280
解析：甲、乙速度和没有改变，所以本题可以利用整体思路进行求解．上午10点到下午1点的3小时中，两车其实行驶的距离就是240千米，那么上午8～10点，这2小时行驶的距离为240÷3×2=160(千米)，故A，B两地的全长为120+160=280(千米)．
2.九一小学有80名学生租了一辆40座的车去海边观看日出．未乘上车的学生步行，和汽车同时出发，汽车往返接送．学校离海边48千米，汽车的速度是学生步行速度的9倍．汽车应在距海边( )千米处返回接第二批学生，才能使学生同时到达海边．(A)
A. 8
B. 12
C. 16
D. 20
E. 24
解析：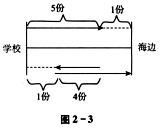
如图2-3所示，汽车到达乘车学生下车的地点又返回到与未乘车学生相遇的地点，汽车所行路程应为未乘车学生步行路程的9倍，因此汽车单程是未乘车学生步行路程的(9+1)÷2=5(倍)．
汽车返回与未乘车学生相遇时，未乘车学生步行的路程与乘车学生步行到海边的路程相等．由此得出从学校到汽车接送乘车学生下车地点的距离为下车点到海边距离的5倍，所以下车点距离海边占全程的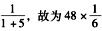
3.甲、乙、丙三人分奖金，三人所得之比为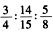
(C)
A. 2850元
B. 2580元
C. 2770元
D. 3050元
E. 3500元
解析：甲所占的比例为
4.已知x，y，z∈R，且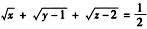
(B)
A. 12
B. 14
C. 16
D. 18
E. 20
解析：
故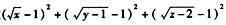
5.关于x的方程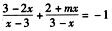
(E)
A. 0．5
B. －0．5
C. 2
D. 8／3
E.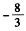 
解析：两边同乘3－x，解得(m+1)x=－2；要想使得方程无解，有两种情况：第一种，m=－1；第二种，x的解恰好为增根3，此时m=
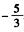故所有满足条件的实数m之和为
6.已知不等式ax2+4ax+3≥0的解集为R，则a的取值范围是( )．(E)
A.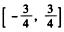 
B. (0，3／4)
C. (0，3／4]
D. [0，3／4)
E. [0，3／4]
解析：当a=0时，3≥0对任意x∈R均成立；
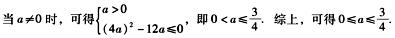
7.设f(x)=x+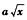
(B)
A. 2个或3个
B. 至少1个
C. 至多1个
D. 0个
E. 1个或2个
解析：假设|f(1)|，|f(4)|，|f(9)|均小于1／2，此时
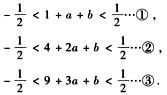
将①式和③式相加得－1＜4a+2b+10＜1
－3＜4a+2b
本文档预览：3000字符，共11439字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载
