管理类专业学位联考综合能力（数学）模拟试卷128

管理类专业学位联考综合能力（数学）模拟试卷128

管理类专业学位联考（综合能力）-问题求解

1.函数f(x)=min{|x|，|x+t|}，对任意实数x，都有f(－x)=f(x－1)，则t的值为( )．(D)

A. －2

B. 2

C. －1

D. 1

E. 3

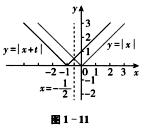
解析：对任意实数x，都有f(－x)=f(x－1)，说明f(x)的图像关于直线x=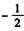对称，如图1-11所示，可以看出，当t=1时，满足对称要求．

2.有甲、乙、丙三人，甲每分钟行70米，乙每分钟行60米，丙每分钟行75米，甲、乙从A地去B地，丙从B地去A地，三人同时出发，丙遇到甲8分钟后，再遇到乙．A，B两地相距( )千米．(C)

A. 14．5

B. 15．37

C. 15．66

D. 15．95

E. 17．4

解析：丙、乙8分钟行的路程是丙、甲相遇时甲比乙多行的路程．

所以A，B两地相距(70+75)×[(75+60)×8÷(70－60)]÷1000=15．66(千米)．

3.某工程队计划用8天完成一项疏通河道的任务，施工中仅用两天时间就完成了工程的40％，则照此速度施工，可提前完工的天数为( )．(B)

A. 4天

B. 3天

C. 2天

D. 1天

E. 0．5天

解析：余下的工程，按计划需用8－2=6(天)完成．余下的工作为60％=3／5，一天的进度为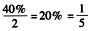，于是，需要天数为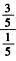

4.已知a+b+c=1且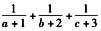(A)

A. 49

B. 64

C. 81

D. 100

E. 121

解析：因为a+b+c=1，所以(a+1)+(b+2)+(c+3)=7．

令p=a+1，q=b+2，r=c+3，则

5.已知2⁴⁸－1可以被60与70之间的两个整数整除，则这两个数为( )．(C)

A. 61，63

B. 61，65

C. 63，65

D. 63，67

E. 64，66

解析：2⁴⁸－1=(2²⁴+1)(2²⁴－1)=(2²⁴+1)(2¹²+1)(2¹²－1)

=(2²⁴+1)(2¹²+1)(2⁶+1)(2⁶－1)=(2²⁴+1)(2¹²+1)×65×63．

6.已知f(x)满足2f(x)+f(1／x)=3x，则f(2)的值为( )．(C)

A. 2

B. 3

C. 3．5

D. 4

E. 4．5

解析：构造方程组法：若已知的函数关系较为抽象简约，则可以对变量进行置换，设法构造方程组，通过解方程组求得函数解析式．

已知2f(x)+f(1／x)=3x ①，

将①中x换成1／x得2f(1／x)+f(x)=3／x ②，

①×2－②得3f(x)=6x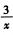－，得到f(x)=2x－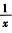

7.不等式3^x+1+2·3^2－x＞29的解集为( )．

B

解析：原不等式即3·3^x+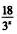＞29，化简整理得3·(3^x)²－29·3^x+18＞0，设t=3^x，则3t²－29t+18＞0，解得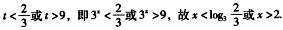

8.若a，b，m都是正实数，且lga＜lgb，则下列不等式中恒成立的是( )．

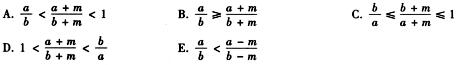(A)

A.

B.

C.

D.

E.

本文档预览：3000字符，共12852字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载