管理类专业学位联考综合能力（数学）模拟试卷129

管理类专业学位联考综合能力（数学）模拟试卷129

管理类专业学位联考（综合能力）-问题求解

1.已知函数f(x)=|2x－a|+|2x－1|+a，当x∈R时，f(x)≥3恒成立，则a的取值范围为( )．(D)

A. a＜1

B. a＜1或a＞2

C. a＞2

D. a≥2

E. a＜2

解析：利用三角不等式|2x－a|+|2x－1|+a≥|2x－a+1－2x|+a=|a－1|+a，所以只需|a－1|+a≥3恒成立即可，①当a≥1时，2a－1≥3

2.甲、乙两车同时从A地开往B地，乙车6小时可以到达，甲车每小时比乙车慢8千米，因此比乙车晚1小时到达．A，B两地间的路程是( )千米．(B)

A. 288

B. 336

C. 386

D. 432

E. 480

解析：行6小时，乙车比甲车多行8×6=48(千米)，而这48千米是甲车行1小时的路程．A，B两地相距：8×6×(6+1)=336(千米)．

3.某车间接到一批任务，需要加工6000个A型零件和2000个B型零件，车间共有224名工人，每人加工5个A型零件所用的时间可以加工3个B型零件．将这批工人分成两组，两组同时工作，每组加工一种型号零件，为了在最短时间内完成任务，应分配来加工B型零件的人数为( )．(B)

A. 90

B. 80

C. 70

D. 60

E. 50

解析：等量关系：这两组工人同时完工，即加工A，B型零件所用的时间相等．

设x人加工A型零件，那么加工B型零件有224－x人，由题意可得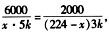

4.已知w²+w+1=0，则w¹⁹⁹³+w¹⁹⁹⁴+w¹⁹⁹⁵+…+w²⁰¹⁹=( )．(B)

A. －1

B. 0

C. 1

D. 2

E. 3

解析：w¹⁹⁹³+w¹⁹⁹⁴+w¹⁹⁹⁵+…+w²⁰¹⁹可以拆分成相邻3个数字为1组的9组数字，比如：

w¹⁹⁹³+w¹⁹⁹⁴+w¹⁹⁹⁵=w¹⁹⁹³(1+w+w²)为一组，提取公因式即可．

5.已知函数f(x)对任意的a，b∈R满足：f(a+b)=f(a)+f(b)－6，且f(－2)=12，则f(2)的值为( )．(A)

A. 0

B. 6

C. －6

D. －12

E. 12

解析：由f(a+b)=f(a)+f(b)－6，令a=b=0，得f(0)=6，

再令a=2，b=－2，得f(2)=0．

6.不等式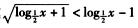

A

解析：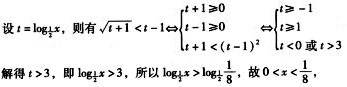

解集为{x|0＜x＜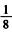

7.设函数f(x)=|2－x²|，若0＜a＜b，且f(a)=f(b)，则ab的取值范围是( )．(A)

A. (0，2)

B. (0，2]

C. [0，2)

D. (0，4)

E. (2，4)

解析：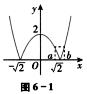

8.已知等差数列{a_n}的前n项和为S_n，若m＞1，且a_m－1+a_m－1－a_m²－1=0，S_2m－1=39，则m=( )．(B)

A. 39

B. 20

C. 19

D. 10

E. 40

解析：数列{a_n}为等差数列，则a_m－1+a_m+1－a_m²－1=2a_m－a_m²－1=－(a_m－1)²=0a_m=1，又因为S_2m－1=(2m－1)a_m=39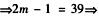

9.等比数列{a_n}的前n项和为S_n，已知S₁，2S₂，3S₃成等差数列，则{a_n}的公比为(

本文档预览：3000字符，共11776字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载