全国自考公共课线性代数（经管类）模拟试卷40

全国自考公共课线性代数（经管类）模拟试卷40

单选题

1.设A、B为n阶可逆矩阵，下列选项等式不成立的是 (D)

A. ｜AB｜＝｜BA｜

B. (AB)^T＝B^TA^T

C. (AB)^-1＝B^-1A^-1

D. (A+B)^-1＝A^-1＋B^-1

解析：因为｜AB｜＝｜A ｜·｜B｜，所以｜AB｜＝｜BA｜＝｜A｜·｜B｜，故A成立．而B、C也都符合矩阵运算的规律，故B、c成立．因此D不成立．

2.设A是n阶矩阵，A^*是A的伴随矩阵，则 ( )(C)

A. AA^*=｜A｜

B. AA^*=｜A｜^*

C. A^*A=｜A｜

D. A^*A=｜A｜^*I

解析：A.A^*=｜A｜I．答案为C.

3.设A为n阶方阵，B是A经过若干次矩阵的初等变换后所得的矩阵，则有 ( )(C)

A. |A|=|B|

B. |A|≠|B|

C. 若|A|=0，则一定有|B|=0

D. 若|A|＞0，则一定有|B|＞0

解析：设B=PAQ，其中P，Q为可逆矩阵，

于是当|A|=0时，|B|=|PAQ|=|P|.|A|.|Q|=0．

故选C．

4.设n阶矩阵A非奇异(n≥2)，A*是矩阵A的伴随矩阵，则 ( )(C)

A. (A*)*=|A|^n-1A

B. (A*)*=|A|ⁿ⁺¹A

C. (A*)*=|A|^n-2A

D. (A*)*=|A|ⁿ⁺²A

解析：AA*=|A|E两边取行列式，得

|A||A*|=|A|ⁿ|E|，又|A|≠0，得|A*|=|A|^n-1．

又(A*)*A*=|A*|E=|A|^n-1E，故(A*)*=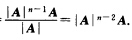

5.设A、B为n阶方阵，且AB=O(零矩阵)，则 ( )(D)

A. A=P或B=O

B. A+B=O

C. ｜A｜+｜B｜=0

D. ｜A｜=0或｜B｜=0

解析：由于｜AB｜=｜A｜．｜B｜=｜0｜=0，所以｜A｜=0或｜B｜=0．答案为D。

6.设A为四阶方阵，若(D)

A. －1

B. 2

C. 1/2

D. 1

解析：

7.已知三阶矩阵A与B相似，且已知A的特征值为1，2，4，则｜B^－1｜ ﹦ (A)

A. 1／8

B. 8

C. 1／7

D. 7

解析：相似矩阵必有相同的特征值，因A～B，则A与B有相同的特征值，即B的特征值为1，2，4，则｜B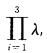｜＝，即｜B｜＝1×2×4＝8，而｜B^-1｜＝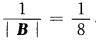

8.实二次型f(x₁，…，x_n)=x^TAx为正定的充要条件是 ( )(B)

A. f的秩为n

B. f的正惯性指数为n

C. f的正惯性指数等于f的秩

D. f的负惯性指数为n

解析：由正定的性质即得．答案为B。

9.设ε₁，ε₂，ε₃是Ax=0的基础解系，则该方程组的基础解系还可以表示成 ( )(C)

A. ε₁，ε₂，ε₃的一个等价向量组

B. ε₁，ε₂，ε₃的一个等秩向量组

C. ε₁，ε₁+ε₂，ε₁+ε₂+ε₃

D. ε₁—ε₂，ε₂一ε₃，ε₃—ε₁

解析：A错误，这是因为等价向量组所含向量的个数不一定相同，如ε₁，ε₂，ε₃，ε₁+ε₂也与ε₁，ε₂，ε₃等价，但它不是基础解系．B也错误，等价自然等秩．C正确，一方面它与ε₁，ε₂，ε₃等价，且另一方面个数也为3．D错误，ε₁一ε₂，ε₂一ε₃，ε₃一ε₁线性相关．

10.设λ₁与λ₂是矩阵A的两个不同的特征值，ε，η是A的分别属于λ₁，λ₂的特征向量，则 ( )(D)

A. 存在常数k₁≠0，k₂≠0，使k₁ε+k₂η是A的特征向量

B. 存在唯一的一组常数k₁≠0，k₂≠0，k₁g+k₂η是A的特征向量

C. 对任意k₁≠0，k₂≠0，k₁ε+k₂η，是A的特征向量

D. 当k₁≠0，k₂≠0时，k₁ε+k₂η不可能是A的特征向量

解析： 假设k₁ε+k₂η是A的属于λ的特征向量，即 A(k₁ε+k₂

本文档预览：3500字符，共13117字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载