全国自考公共课线性代数（经管类）模拟试卷46

全国自考公共课线性代数（经管类）模拟试卷46

单选题

1.设A=(C)

A. 2x=7

B. 2y=x

C. y=x+1

D. y=x一1

解析：由于

2.若齐次线性方程组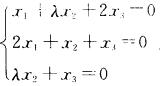(B)

A. λ=一1

B. λ≠一1

C. λ=1

D. λ≠1

解析：齐次线性方程组Ax=0只有零解→｜A｜≠0

｜A｜=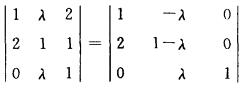

3.二次型f=x^TAx经过满秩线性变换x=Py可化为二次型y^TBy，则矩阵A与B ( )(A)

A. 一定合同

B. 一定相似

C. 即相似又合同

D. 即不相似也不合同

解析：x^TAx=(Py)^TA(Py)=y^T(P^TAP)y=y^TBy，即B=p^TAp，所以矩阵A与B一定合同．只有当P是正交矩阵时，由于P^T=P^-1，所以A与B既相似又合同．答案为A.

4.二次型f＝x₁²＋x₂²＋x₃²＋4x₂x₃的规范形是 (C)

A. z₁²＋z₂²+₃²

B. z₁²－z₂²－z₃²

C. z₁²＋z₂²﹣z₃²

D. z₁²－z₂²

解析：

5.设n维向量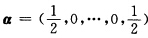(C)

A. O

B. 一E

C. E

D. E+α^Tα

解析：B=(E—α^Tα)(E+2α^Tα)

=E+α^Tα一2α^Tαα^Tα

=E+α^Tα一2α^T(αα^T)α

=E+α^Tα一2×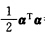

6.设A为n阶方阵，B是A经过若干次矩阵的初等变换后所得的矩阵，则有 ( )(C)

A. |A|=|B|

B. |A|≠|B|

C. 若|A|=0，则一定有|B|=0

D. 若|A|＞0，则一定有|B|＞0

解析：设B=PAQ，其中P，Q为可逆矩阵，

于是当|A|=0时，|B|=|PAQ|=|P|.|A|.|Q|=0．

故选C．

7.设向量组α₁，α₂，α₃线性无关，则下列向量组线性相关的是 ( )(C)

A. α₁+α₂，α₂+α₃，α₃+α₁

B. α₁，α₁+α₂，α₁+α₂+α₃

C. α₁一α₂，α₂一α₃，α₃一α₁

D. α₁+α₂，2α₂+α₃，3α₃+α₁

解析：显然(α₁一α₂)+(α₂一α₃)+(α₃一α₁)=0．

8.设β，α₁，α₂线性相关，β,α₂，α₃线性无关，则 ( )(C)

A. α₁，α₂，α₃线性相关

B. α₁，α₂，α₃线性无关

C. α₁可以用β，α₂，α₃线性表示

D. β可以用α₁，α₂，α₃线性表示

解析：β，α₂，α₃线性无关，自然β，α₂也线性无关，β，α₁，α₂线性相关，故存在不全为零的数k₁，k₂，k₃使得k₁β+k₂α₁+k₃α₂=0，又β，α₂线性无关，故k₂≠0(否则k₁，k₂都为0)，故

9.零为矩阵A的特征值是A不可逆的 ( )(D)

A

本文档预览：3500字符，共12670字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载