教师公开招聘考试中学数学（解析几何）模拟试卷8

教师公开招聘考试中学数学（解析几何）模拟试卷8

选择题

1.过点A(1，—2)和B(3，0)且圆心在直线y=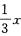(B)

A. (x—3)²+y²=8

B. (x—3)²+(y+2)²=4

C. (x—3)²+(y+2)²=8

D. (x—3)²+(y—2)²=4

解析：设这个圆的圆心坐标为(a，b)，则点A、B到圆心的距离相等，且圆心在直线y=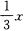—3上，故有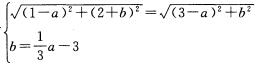，化简得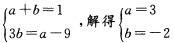，则圆心坐标为(3，—2)，半径r=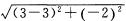

2.已知椭圆的方程为3x²+k²y²=15k²，且其焦点在y轴上，那么k的取值范围是( )．

(D)

A.

B.

C.

D.

解析：由题，椭圆方程可化简为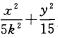=1(k≠0)．因为焦点在y轴上，所以5k²＜15，解得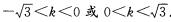

3.已知二元一次方程3x²—7x+2=0的两根分别为椭圆和双曲线的离心率e₁、e₂，则3(e₂—e₁)=( )．

(B)

A.

B.

C.

D.

解析：求解3x²—7x+2=0的两根为x₁=2，x₂=．因为椭圆的离心率0＜e₁＜1，双曲线的离心率e₂＞1，故e₁=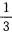，e₂=2，3(e₂—e₁)=3×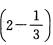

4.已知平面直角坐标系中有四点，A(0，0)，B(1，2)，C(—3，—6)，D(—2，1)，过这四点中任两点作直线，其中相互垂直的直线有( )对．(B)

A. 0

B. 1

C. 2

D. 3

解析：根据题干可知点B和点C的坐标成倍数关系，则求得过这两点的直线为y=2x，且直线过原点，所以点A、B、C在一条直线上，过这四点可作四条直线．过两点的直线的斜率公式为k=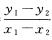，代入各点坐标运算得，k_BC=2，k_CD=7，k_BD=，k_AD=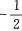

5.直线2y—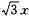+6=0与x轴交于点P，已知点P在圆x²+(y+2)²=25内，过点P的一条直径被点P分为两段，则较短的一段与较长的一段的比值为( )．

(A)

A.

B.

C.

D.

解析：已知直线方程为2y—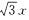+6=0，则与x轴的交点P的坐标为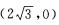．由圆的方程可知，圆心坐标为(0，—2)，半径为5．点P到圆心的距离为d=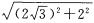=4，则点P与所在直径的一端距离为r—d=1，与另一端距离为r+d=9，故两段的比值为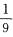

6.已知双曲线的离心率为3，且左焦点F₁的坐标为(—3，0)．若双曲线上有一点M，满足MF₁⊥x轴，则△MF₁F₂的面积等于( )．

本文档预览：3500字符，共12787字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载