教师公开招聘考试小学数学（应用题）模拟试卷3
综合题
某产品按行业生产标准分为8个等级，等级系数X依次为1，2，…，8，其中X≥5为标准A，X≥3为标准B．已知甲厂执行标准A生产该产品，产品的零售价为6元／件；乙厂执行标准B生产该产品，产品的零售价为4元／件．假定甲、乙两厂的产品都符合相应的执行标准．
1.已知甲厂产品的等级系数X1的概率分布列如下所示：
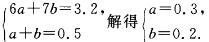
因为EX1=6，所以5×0．4+6a+7b+8×0．1=6，即6a+7b=3．2．
又由X1的概率分布列得0．4+a+b+0．1=1，即a+b=0．5．由[*]
解析：
2.为分析乙厂产品的等级系数X2，从该厂生产的产品中随机抽取30件，
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布，将频率视为概率，求等级系数X2的数学期望；
由已知得，样本的频率分布表如下：
[*]
用这个样本的频率分布估计总体分布，将频率视为概率，可得等级系数X2的概率分布列如下：
[*]
所以EX2=3×0．3+4×0．2+5×0．2+6×0．1+7×0．1+8×0．1=4．8．
即乙厂产品的等级系数的数学期望等于4．8．
解析：
3.在(Ⅰ)、(Ⅱ)的条件下，若以“性价比”为判断标准，则哪个工厂的产品更具可购买性?说明理由．
注：(1)产品的“性价比”=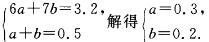
乙厂产品更具有可购买性，理由如下：
因为甲厂产品的等级系数的数学期望等于6，价格为6元／件，所以其性价比为[*]=1．
因为乙厂产品的等级系数的数学期望等于4．8，价格为4元／件，所以其性价比为[*]=1．2．
因此，乙厂的产品更具可购买性．
解析：
按照某学者的理论，假设一个人生产某产品的单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为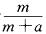
；如果他买进该产品的单价为n元，则他的满意度为
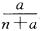如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2，则他对这两种交易的综合满意度为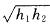
4.求h甲和h乙关于mA、mB的表达式；当mA=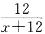
设mA=x，mB=y．
(Ⅰ)甲买进产品A的满意度：h1甲=[*]；甲卖出产品B的满意度：h2甲=[*]；甲买进产品A和卖出产品B的综合满意度：h甲=[*]同理，乙卖出产品A和买进产品B的综合满意度：h乙[*].h乙=[*].故h甲=h乙．
解析：
5.设mA=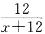
当x=[*]y时，由(1)知h甲=h乙=[*]
当且仅当y=10等号成立．当y=10时，x=6．因此，当mA=6，mB=10时，甲、乙两人的综合满意度均最大，且最大的综合满意度为[*].
解析：
6.设(Ⅱ)中最大的综合满意度为h0，试问能否适当选取mA、mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立?试说明理由．
由(Ⅱ)知h0=[*]因为h甲h乙=[*]，所以，当h甲≥[*]，h乙≥[*]时，有h甲=h乙=[*]因此，不能取到MA，MB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立．
解析：
甲、乙两家商场进行促销活动，甲商场采用“买200减100”的促销方式，即购买商品的总金额满200元但不足400元，少付100元，满400元但不足600元，少付200元；…，乙商场按总金额打6折促销．
7.若顾客在甲商场购买了510元的商品，付款时应付多少钱?
根据题意得：510—200=310(元)．
答：顾客在甲商场购买了510元的商品，付款时应付310元．
解析：
8.若顾客在甲商场购买商品的总金额为x(400≤x＜600)元，优惠后得到商家的优惠率为p(p=
p与x之间的函数关系式为p=[*]，p随x的增大而减小．
解析：
9.品牌、质量、规格等都相同的某种商品，在甲乙两商场的标价都是x(200≤x＜400)元，你认为选择哪家商场购买商品花钱少?请说明理由．
设购买商品的总金额为x元，(200≤x＜400)，则甲商场需花x－100元，乙商场需花0．6x元，
由x－100＞0．6x，得：250＜x＜400，乙商场花钱较少，
由x－100＜0．6x，得：200≤x＜250，甲商场花钱较少，
由x－100=0．6x，得：x=250，两家商场花钱－样多．
解析：
10.如图，某住宅小区的平面图呈圆心角为120°的扇形AOB，小区的两个出入口设置在点A及点C处，且小区里有一条平行于BO的小路CD，已知某人从C沿CD走到D用了10分钟，从D沿DA走到A用了6分钟，若此人步行的速度为每分钟50米，求该扇形的半径OA的长(精确到1米)．
