管理类专业学位联考综合能力（数学）模拟试卷123

管理类专业学位联考综合能力（数学）模拟试卷123

管理类专业学位联考（综合能力）-问题求解

1.长途汽车从A站出发，匀速行驶1小时后突然发生故障，车速降低了40％，到B站终点延误达3小时，若汽车能多跑50千米后，才发生故障，坚持行驶到B站能少延误1小时20分钟，那么A，B两地相距( )．(E)

A. 412．5千米

B. 125．5千米

C. 146．5千米

D. 152．5千米

E. 137．5千米

解析：设原来车速为v千米／小时，则有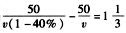

2.某筑路队按照原施工方法制定了施工计划．工作了4天后改用新施工方法，由于新施工方法比旧施工方法提高效率50％，因此比原计划提前1天完成．如果用旧施工方法筑了200米后再改用新施工方法，就可以比原计划提前2天完工．则原计划每天可以施工( )米．(B)

A. 100

B. 200

C. 300

D. 400

E. 600

解析：新施工方法效率提高50％，则新效率∶旧效率=3∶2．那么，工作4天后剩下的工作量用原计划与现计划的时间之比为3∶2，此时正好差1天，那么原计划总共需要7天．

若是先修了200米之后，二者相差2天，那么剩余工作量原计划还需做6天，现计划还需做4天，可知原计划1天的施工量为200米．

3.已知a＞0，b＞0，a+b=1，则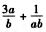(D)

A. 2

B. 4

C. 5

D. 6

E. 8

解析：当看到分子和分母的次数不一样时，可以采用“1”的妙用——齐次化的技巧来进行求解．

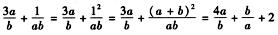
此时利用均值定理：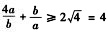

4.已知(2x－1)⁶=a₀+a₁x+a₂x²+…+a₆x⁶，则a₂+a₄+a₆=( )．(C)

A. 360

B. 362

C. 364

D. 366

E. 368

解析：令x=1，有 1=a₀+a₁+a₂+…+a₆ ①

再令x=－1，有 3⁶=a₀－a₁+a₂－…+a₆ ②

①+②后再除以2得到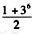

5.已知函数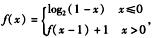(A)

A. 2020

B. －2020

C. 1

D. －1

E. 0

解析：依题可得，f(2020)=f(2019)+1=…=f(0)+2020=2020，选A．

6.设函数以zf(x)=min{x²－1，x+1，－x+1}，其中min{x，y，z}表示x，y，z中的最小者．若f(a+2)＞f(a)，则实数a的取值范围为( )．(D)

A. (－∞，－3)∪(－1，O)

B. (－∞，－2)

C. (－1，0)

D. (－∞，－2)∪(－1，0)

E. (－∞，－2)∪(0，1)

解析：当a+2≤－1时，a＜a+2≤－1，此时有f(a)＜f(a+2)；

当－1＜a+2＜0时，－3＜a＜－2，此时有f(a)＜f(－2)=－1＜f(a+2)；

当0≤a+2≤1时，－2≤a≤－1，此时有f(a)≥f(a+2)；

当1＜a+2＜2时，－1＜a＜0，此时有f(a)＜f(a+2)；

当a+2≥2时，a≥0，此时有f(a)≥f(a+2)．

7.已知数列{a_n}的各项均为正数，{b_n}满足b_n=㏒₂a_n，n∈Z₊，其中{b_n}为等差数列，a₁₀a₂₀₁₅=2，则b₁+b₂+…+b₂₀₂₄=( )．(C)

A. 1010

B. 1011

C. 1012

D. 1013

E. 1014

解析：令数列{a_n}的每一项均为x，则a₁₀a₂₀₁₅=x²=2，a_n=x=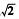，b_n=㏒₂a_n=1／2，故b₁+b₂+

本文档预览：3000字符，共12516字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载