管理类专业学位联考综合能力（数学）模拟试卷118

管理类专业学位联考综合能力（数学）模拟试卷118

管理类专业学位联考（综合能力）-问题求解

1.x∈[2，5]，|a|=5－x，|b|=x－2，则|b－a|的取值范围为( )．(E)

A. [－3，5]

B. [0，5]

C. [1，3]

D. [3，5]

E. [0，3]

解析：利用三角不等式||a|－|b||≤|a－b|≤|a|+|b|，则最大值|a|+|b|=3．最小值不能为负，最小为0；故|b－a|=|2x－7|∈[0，3]．

2.在田径场上，甲跑10米的时间乙只能跑7米，现在甲、乙两人同时同向从起点出发，当甲第二次追及乙时，乙跑的圈数为( )．(B)

A. 7／3

B. 14／3

C. 3

D. 11／3

E. 2

解析：依题意有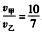，因为两人相遇时，所耗时间相同，所以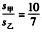，由于甲比乙总是多跑田径场的整数圈，可设n为甲追及乙的次数，l为跑道的长度，所以s_甲－s_乙=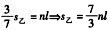根据题意，当n=2时，s_乙=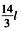

3.24头牛6天可以将一片牧草吃完，21头牛8天可以将这片牧草吃完．如果每天草的增长量是相等的，为了防止草场退化，最多放养( )头牛吃这片草，才能保证牧草永远不会被吃完．(A)

A. 12

B. 24

C. 36

D. 8

E. 10

解析：只要草地上原有的草量在减少，总有一天牧草会被吃完，因此，要使这片牧草永远不被吃完，也就是草地上原有的草量不能减少．那么牛数最多的情况就是牛吃的草等于草新增长的量．

根据题意，假设每头牛每天吃的草为单位“1”，草每天生长的量为：(21×8－24×6)÷(8－6)=12；所以最多放养12头牛．

4.设a，b，c为三个相异实数，且f(x)=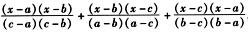(C)

A. 2000

B. 4046

C. 2023

D. 1012

E. 3000

解析：因为f(x)为二次函数形式，三个点可以确定其表达式，而f(a)=1，f(b)=1，f(c)=1，所以f(x)=1，即f(1)=1，…，f(2023)=1，则有

f(1)+f(2)+f(3)+…+f(2023)=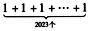

5.若0＜x＜1，则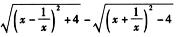(D)

A. 2／x

B. 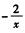C. －2x

D. 2x

E. 3x

解析：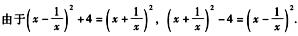

又因为0＜x＜1，所以x+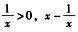＜0．

故原式=x+

6.f(x)=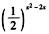(B)

A. 1

B. 2

C. 3

D. 4

E. 8

解析：由于x²－2x=(x－1)²－1≥－1，f(x)是底为1／2(＜1)的指数函数，函数递减，则最大值是2．

7.给出函数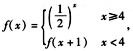(E)

A. 3／20

B. 1／3

C. 1／4

D. 1／8

E. 1／24

解析：f(x)为分段函数，㏒₂3＜㏒₂2⁴=4，㏒₂3+1=㏒₂6＜㏒₂2⁴，

㏒₂6+1=㏒₂12＜㏒₂2⁴，㏒₂12+1=㏒₂24＞㏒₂2⁴，

f(㏒₂3)=f(㏒₂2

本文档预览：3000字符，共12753字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载