
全国自考教育评估和督导(计算题、论述题)模拟试卷1
计算题
1.请20位专家对5项指标的重要程度进行判断,结果统计如下表:
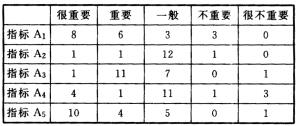
(1)A1指标的加权平均值是:
(8×5+6×4+4×3+4×2+0×1)/20=3.95
同理,可知A2,A3,A4,A5的加权平均值分别是2.35,3.55,3.10,4.10。
(2)通过归一化处理可得
A1,A2,A3,A4,A5的权重分别是:0.23,0.14,0.21,0.18,0.24。
这轮调查后可知,最为重要的两项指标是A5和A1。
解析:
2.向4位专家发函征求意见,让每一位专家对5项指标的权重进行分配,第一轮调查结果如表1(表中数据为权重):
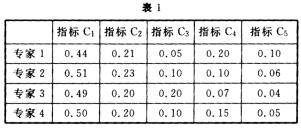
现在要将第一轮权重调查的统计结果按表2形式反馈给其中的第3位专家。请在表2中的空缺处填写出相应的统计结果,并写出主要的计算公式或计算过程及其结果。(结果保留三位小数)

(1)计算C4的权重平均值
=ln∑Wij=0.130
或(0.20+0.10+0.07+0.15)/4=0.130
(2)计算第3位专家指标C2的估计值离差:
△ij=Wij-(Wi)(j=1,2,…m)=-0.010
或0.20-0.210=-0.010。
解析:
3.请15位专家对4个指标的重要程度进行判断,结果统计如下表:
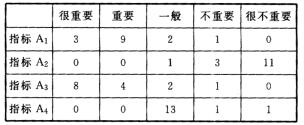
(1)A1指标的加权平均值是:
(3×5+9×4+2×3+1×2+0×1)/15=3.93
同理,可知A2,A3,A4的加权平均值分别是1.33.4.27,2.80。
(2)通过归一化处理可得:
A1,A2,A3,A4的权重分别是0.32,0.11,0.34,0.23。
解析:
4.用层次分析法确定权数。两两比较的结果如下表:
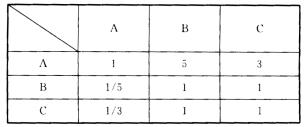
(1)对每列数据进行归一化处理
1+1/5+1/3=23/15
1÷23/15=15/23 1/5÷23/15=3/23
1/3÷23/15=5/23
0.652 0.714 0.60
0.131 0.143 0.20
0.217 0.143 0.20
(2)对上面矩阵各行数据求和
第一行1.966
第二行0.474
第三行0.560
对上面求和得出的数据进行归一化处理,得出A,B,C的权数分别为0.66,0.16,0.18。
解析:
5.用特尔斐法确定权重。请20位专家对4个指标(C1;C2、C3、C4)的重要程度进行判断,结果统计如下表:
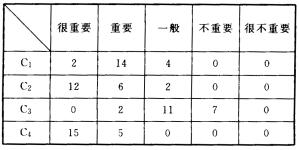
(1)C1指标的加权平均值是(2×5+14×4+4×3)÷20=3.90
同理可知C2,C3,C4的加权平均值分别是4.50,2.75,4.75。
(2)通过归一化处理可得
C1、C2、C3、C4的权重分别为:0.25,0.28,0.17,0.30。
解析:
6.有人向4位专家发函征求意见,让每一位专家对4项指标的权重进行分配,第一轮调查结果如表1(表中数据为权重):
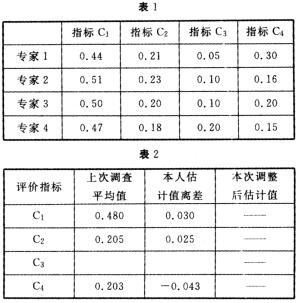
(1)计算C3的权重平均值
=ln∑ni=1Wij=0.113
或(0.05+0.10+0.10+0.20)/4=0.113
(2)计算第2位专家指标C3的估计值离差
△ij=Wij-(Wi)(j=1,2,…m)=-0.013
或0.10>0.113=-0.013。
解析:
7.向6位专家发函征求意见,让每一位专家对3项指标的权重进行分配,第一轮调查结果如表1(表中数据为权重):
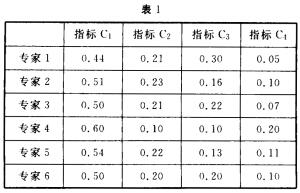
现在要将第一轮权重调查的统汁结果按表2形式反馈给其中的第6位专家。请在表2中的空缺处填写出相应的统计结果,并写出主要的计算公式或计算过程及其结果。(结果保留三位小数)
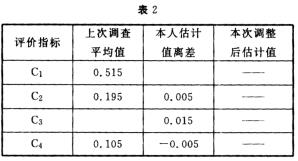
(1)计算C3的权重平均值
=ln∑Wij=0.185
或(0.30+0.16+0.22+0.10+0.13+0.20)/6=0.185
(2)计算第3位专家指标C1的估计值离差
△ij=Wij-(Wi)(j=1,2,…m)=-0.015
或0.50-0.515=-0.015。
解析:
8.某中学高二(1)(2)(3)(4)四个班人数分别是66,61,64,60,期中考试四个班的数学平均分分别是131,126,124和130。请计算出这次期中考试四个班数学的总平均分,结果保留两位小数。
[*]=∑Wi.Xi/∑Wi
=(66×131+61×126+64×124+60×130)/
(66+61+64+60)
本文档预览:3500字符,共15928字符,源文件无水印,下载后包含无答案版和有答案版,查看完整word版点下载