考研数学二（高等数学）模拟试卷156

考研数学二（高等数学）模拟试卷156

选择题

1.设a_n=∫₀¹x_n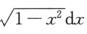，b_n=∫₀^π/2sinⁿtdt，则极限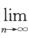(C)

A. 0

B. e

C. e^-1

D. +∞

解析：a_n=∫₀¹x_n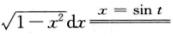∫₀^π/2sinⁿ t·cos²tdt=∫₀^π/2sinⁿt(1-sin²t)dt=b_n-b_n+2．

又b_n+2=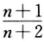b_n，则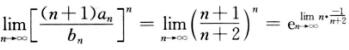

2.曲线y=e^．+x⁵的极值点与拐点个数分别为（ ）．(A)

A. 0，1

B. 1，1

C. 0，3

D. 1，5

解析：对y=e^x+x⁵两边关于x求导，得

y’=e^x+5x⁴。

由于y’＞0恒成立，故y无极值点．对y’=e^x+5x⁴两边关于x求导，得

y\\

3.曲线x²+xy+y²=1在点(1，-1)处的曲率为（ ）．

B

解析：由题意，将x²+xy+y²=1两端同时对x求导，得

再将上式两端同时对x求导，得

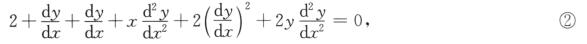
将x=1,y=-1代入①式得dy/dx=1．将x=1,y=-1，dy/dx=1代入②式得d²y/dx²=6，由曲率计算公式得

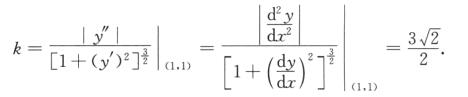
4.设函数f(x)在[0，1]上二阶可导，且∫₀¹f(x)dx=0，则（ ）．(D)

A. 当f’(x)＜0时，f(1/2)＜0

B. 当f\\

C. 当f’(x)＞0时，f(1/2)＜0

D. 当f\\

解析：f(x)在[0，1]上二阶可导，则由带拉格朗日余项的泰勒公式有

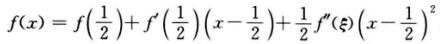
其中ξ介于x与1/2之间．又在[0，1]上取积分得

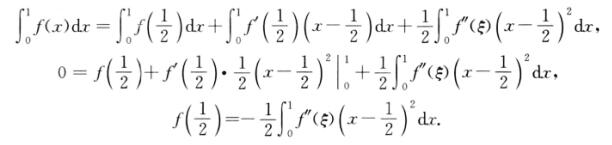
5.设b＞a＞0，函数f(x)在[a，b]上可导，且f’(x)＜2f(x)/x，则当x∈(a，b)时，有不等式（ ）。(A)

A. a²f(x)＜x²f(a)

B. b²f(x)＜x²f(b)

C. x²f(x)＜a²f(a)

D. x²f(x)＞b²f(b)

解析：令F(x)=f(x)/x²，则

6.已知∫₀²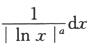(B)

A. 1＜a≤2

B. a＜1

C. 1≤a＜2

D. a＞2

解析：∫₀²

其奇点为-∞，0，为混合型反常积分．

因此拆分原式为

本文档预览：3000字符，共11349字符，源文件无水印，下载后包含无答案版和有答案版，查看完整word版点下载